Классификация системы ОДУ с кубическими возмущениями

[Red_Herring]

Классифицировать точку $(0,0)$ для системы

$$ \left\{\begin{aligned} y'=&\hphantom{-}x + ay^3,\\ x'=&-y +b x^3 \end{aligned}\right. $$

$a$ и $b$ числовые параметры и ответ зависит от них. Читая осенью ОДУ я дал это в лекциях как пример функции Ляпунова.

[мат-ламер]

У меня пока такое предположение. Если $a$ и b одного знака, то ответ находится легко. В качестве функции Ляпунова можно взять $V(x,y)=x^2+y^2$ . Дифференцируя её - $(x^2+y^2)'=2bx^4+2ax^4$ , получаем, что если $a>0$ , $b>0$ , то система неустойчива, а если $a<0$ , $b<0$ , то система устойчива. Пусть теперь $a>0$ и $b<0$ . Допустим система устойчива по $x$ . Тогда получается, что она неустойчива по $y$ . То есть, если $a$ и $b$ разных знаков, то система тоже неустойчива. Возможно её траектории превращаются в этом случае во всё более вытянутые эллипсы.

[Red_Herring]

Я советую в таких случаях выработать правильную гипотезу с помощью графического ОДУ калькулятора, например
https://aeb019.hosted.uark.edu/pplane.html

[мат-ламер]

мат-ламер в сообщении #1520343 писал(а):

Дифференцируя её - $(x^2+y^2)'=2bx^4+2ax^4$ ,

Тут маленькая опечатка - $(x^2+y^2)'=2bx^4+2ay^4$ . Случай разных знаков $a$ и $b$ пока непонятен для меня. Фазовые портреты со стрелочками не помогли. По любому для малых $x$ и $y$ картинка похожа на окружность. Но это не доказательство.

Пока предположу гипотезу. Устойчивость будет зависеть от знака наибольшего по модулю $a$ и $b$ . То есть, если максимальное по модулю из этих чисел отрицательно, то система будет устойчивой, а если положительно, то нет. Если числа разных разных знаков и равны по модулю, то наверное будет фокус, т.е. устойчиво, но не асимптотически.

[Red_Herring]

А почему бы не подправить $x^2+y^2$ членами четвертого порядка, чтобы справа стояло выражение либо строго положительное, либо строго отрицательное вне $0$? Мне фазовые портреты помогли, и очень хорошо.

мат-ламер в сообщении #1520379 писал(а):

то наверное будет фокус, т.е. устойчиво, но не асимптотически.

Разве это фокус?

[demolishka]

Решение.

(Оффтоп)

Возьмём

$$V(x,y)=x^{2}+y^{2} + 2(a - b) (xy^3+yx^3).$$

Тогда $\dot{V}(x,y) = 2(a+b) (x^{4} + y^{4}) + \ldots$, где $\ldots$ обозначает члены порядка $6$. Отсюда при $a+b<0$ получаем асимптотическую устойчивость, а при $a+b>0$ неустойчивость.

UPD: Немного ошибся в вычислениях. Правильная функция такая:

$$V(x,y) = 3(x^{2}+y^{2}) + 2(a-b)(xy^{3}+yx^{3}) + 2axy^{3}-2b yx^{3}.$$

Тут конечно системы компьютерной алгебры не помогают (в окрестности нуля всё очень кругло). Вот если руками нарисовать, что происходит возле исходных окружностей:

[мат-ламер]

Red_Herring в сообщении #1520384 писал(а):

Разве это фокус?

Опечатака, сильно спешил, дела по дому. Центр, конечно.

P.S. "конечно " - это, когда писал, думал про центр. Но что это действительно центр, то надо ещё доказать.

[Red_Herring]

demolishka в сообщении #1520388 писал(а):

Решение.

Да. А при $a+b=0$ есть интегрирующий множитель $\mu (x,y)=f(xy)$.

[sup]

demolishka
А как Вы искали это решение?
Хотелось бы иметь какое-нибудь "технологичное" решение. Чтобы не надо было ничего угадывать.
Мне кажется, что в данном случае такой подход имеется.
Систему легко свести к виду

$$ \left\{\begin{aligned} y'=&\hphantom{-}x + \lambda ay^3,\\ x'=&-y +\lambda b x^3, \end{aligned}\right. $$

где $\lambda \to 0$.
Будем рассматривать решения с начальными данными $y(0) = 0$, $x(0) = 1$. Тогда имеем

$$ x(t) \sim \cos t, \quad y(t) \sim \sin t. $$

Дифференцируем по параметру в точке $\lambda = 0$

$$ \left\{\begin{aligned} u'=&\hphantom{-}v + a\sin^3 t,\\ v'=&-u +b \cos^3 t, \end{aligned}\right. $$

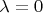
Откуда имеем равенства

$$ (u \cos t - v \sin t)' = a\cos t \sin^3 t - b\sin t \cos^3 t, $$

$$ (u \sin t + v \cos t)' = a \sin^4 t + b\cos^4 t. $$

Осталось только проинтегрировать эти равенства по $t \in (0, 2\pi)$. По-видимому, отсюда можно как-то получить и Вашу функцию $V$.
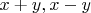
Такой подход "не берет" случай $a + b =0$. С ним я разбирался с помощью перехода к переменным $x+y, x- y$ и соображений симметрии.

[demolishka]

sup в сообщении #1520455 писал(а):

А как Вы искали это решение?

Практически угадыванием , последовав совету добавить в функцию Ляпунова члены четвертого порядка. Я сначала добавил $2a x y^{3}$, чтобы убить слагаемое $2a y^{4}$ при дифференцировании $V(x,y)=x^{2}+y^{2}$ и получил слагаемое $2bx^{4}$ + члены высшего порядка. Потом прибавил только $-2b y x^{3}$ и получил $2 a y^{4}$. Потом решил собрать полную квадратичную форму. Ответ, типа $a + b < 0$ для устойчивости у меня еще до построения функции Ляпунова появился после попыток нарисовать фазовый портрет для разных знаков. Я вот из-за этого даже в своем решении выше неправильную функцию написал, так как получил $a+b$, а вычисления перепроверять не стал . Правильная (надеюсь, что теперь не ошибся) функция Ляпунова будет такой:

(Оффтоп)

$$V(x,y) = 3(x^{2}+y^{2}) + 2(a-b)(xy^{3}+yx^{3}) + 2axy^{3}-2b yx^{3}.$$

[sup]

Пан-нятна
Ну, в таком случае мое решение мне "больше нравится". Не то чтобы я совсем против интуиции и поиска, но технологичность перевешивает. Кстати, подобные соображения можно применять и для других полиномиальных нелинейностей.

[Red_Herring]

demolishka в сообщении #1520457 писал(а):

Правильная (надеюсь, что теперь не ошибся) функция Ляпунова будет такой:

Там для коэффициентов при $x^3y$ и $xy^3$ целый спектр.

sup в сообщении #1520458 писал(а):

Ну, в таком случае мое решение мне "больше нравится".

У меня эта задача родилась в качестве иллюстрации функции Ляпунова, т.ч. другие подходы не годились

[sup]

Red_Herring в сообщении #1520508 писал(а):

У меня эта задача родилась в качестве иллюстрации функции Ляпунова, т.ч. другие подходы не годились

Да, конечно. Я про свое решение высказался вовсе не в качестве критики.
На самом деле мне было просто лень подыскивать подходящую функцию
Разумеется, это не значит, что таким вещам не стоит учиться.

[Padawan]

sup в сообщении #1520455 писал(а):

Откуда имеем равенства

$$ (u \cos t - v \sin t)' = a\cos t \sin^3 t - b\sin t \cos^3 t, $$

$$ (u \sin t + v \cos t)' = a \sin^4 t + b\cos^4 t. $$

Осталось только проинтегрировать эти равенства по $t \in (0, 2\pi)$.

Поясните, пожалуйста, для тупых, что дают эти равенства (проинтегрированные)?

-- Пн май 31, 2021 16:58:31 --

sup в сообщении #1520455 писал(а):

По-видимому, отсюда можно как-то получить и Вашу функцию $V$.

Тоже так думаю. Сейчас метод вытаскивания функции Ляпунова разработаем :)

-- Пн май 31, 2021 17:04:42 --

Правильно ли я понимаю, что для любого полиномиального возмущения системы

$$ \left\{\begin{aligned} y'=&\hphantom{-}x + P(a,b,x,y)\\ x'=&-y +Q(a,b,x,y) \end{aligned}\right. $$

существует (полиномиальная?) функция $R(a,b)$ такая, что система устойчива ттт $R(a,b)>0$?

[GAA]

Если не обсчитался, то первая ляпуновская величина $L_1 = \int_0^{2\pi} (b\cos^4\varphi + a \sin^4 \varphi) d\varphi = \frac 3 4 \pi (a+b)$.
Следовательно:

• если $L_1 <0$, т.е. $a+b <0$, то точка покоя — устойчивый фокус;
• если $L_1 >0$, т.е. $a+b >0$, то точка покоя — неустойчивый фокус;
• если $L_1 =0$, то требуется рассмотреть $L_2 $ и возможно величины более высокого порядка.

Однако интуиция подсказывает, то при $a+b =0$ будет центр. И действительно при $a+b =0$ интеграл находится в элементарных функциях [уравнение для фазовых кривых интегрируется в элементарных функциях], и фазовые кривые являются замкнутыми линиями, окружающими точку покоя.