Не будут.
Если результат есть, то хорошо бы обоснование более аккуратно изложить.
По поводу априорных оценок.
Чтобы не запутаться, я себе напомню, что погрешности при обработке экспериментальных данных могут быть двух типов:
A) погрешностей измерений (о которых нам в данном случае ничего не известно);
B) погрешности вычислений;
Во втором случае грубо предположим, что предельная относительная погрешность составляет

, где

— приблизительно равно 7 для одинарной точности (Single) и 15 для двойной точности (Double). Здесь предполагается, что данные не содержат денормализованные значения (и банальные оговорки про

,

, NaN).
Поскольку о погрешностях измерений нам ничего не известно, то пока нас интересуют погрешности вычислений (B).
Предельная абсолютная погрешность суммы не превосходит суммы предельных абсолютных погрешностей слагаемых. Грубо предельная абсолютная погрешность среднего не превосходит произведения среднего на

. В худшем случае предельная абсолютная погрешность не превосходит

, где
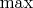
— модуль максимального числа (Single/Double). Для Single предельная абсолютная погрешность будет не превышать

. Банально: на этом пути нужны оценки сверху модуля значений экспериментальных данных. Если значения не превышают 1, то предельная абсолютная погрешность будет меньше

.
[Возражение, что при больших значениях данных мы среднее не сможем получить, т.к. произойдёт переполнение, отметается тем, что при сложении больших чисел заранее выполняется деление на число слагаемых. Технически число слагаемых можно подсчитать по известному формату двоичного файла и его размеру. Если файл текстовый, то конечно нужно знать число точек, но это обычно известно с высокой точностью: данные же сами получали.]
Если слагаемые одного знака, то предельная относительна погрешность среднего не превышает наибольшей из предельных абсолютных относительных погрешностей слагаемых. Грубо для Single предельная относительная погрешность среднего не превысит

.
Если слагаемые разного знака, то среднее может быть равно нулю и относительная погрешность сверху не ограничена.
Ясно, что в практических ситуациях так плохо не бывает, но что-то нужно предположить для получения априорных оценок.
В общем, всё
выше написанное в этом сообщении чудовищно банально. Содержательных мыслей у меня нет. Никаких идей из предыдущих нескольких сообщений я выудить не смог. [Вообще, всё это что-то из самого часто встречаемого на практике. Если никаких чудесных правил на все случаи жизни не предложено, то шанс быстренько предложить формулу всего очень мал. Тут, как всегда, если что-то и можно предположить, то учитывая сведения о данных.]