Выпуклые функции: Очевидно, но...

[трапезун]

Пожалуйста, помогите доказать.


Пусть функция $f$ выпукла на промежутке $I \subset \mathbb{R}$. Показать:
1) что если $f$не равна постоянной, то она не может достигать своей верхней грани во внутренних точках промежутка $I$.
2) что если множество $I$ относительно компактно, то $f$ ограничена снизу на $I$.
3) что если $I= \mathbb{R}$ и $f$ не равна постоянной, то $f$ не ограничена на $I$.

[zkutch]

Ну, "очевидно" это очень многозначное слово и опасно, с одной стороны, им увлекаться и, с другой стороны, не стоит огорчаться из-за него.

А в связи с вашими задачами, например, в 1) случае, попробуйте доказать эквивалентное предложение: для выпуклой на отрезке функции если она достигает во внутренней точке своей верхней грани, то она постоянна.

[трапезун]

Ничего не получается
Ребята, помогите справиться.

[Сергей Михайлов]

трапезун писал(а):

Ничего не получается
Ребята, помогите справиться.

что такое "множество относительно компактно"?

[ruan]

трапезун писал(а):

Пожалуйста, помогите доказать.
Пусть функция $f$ выпукла на промежутке
$I\subset\mathbb{R}$.
Показать:
1) что если $f$не равна постоянной, то она не может достигать своей верхней грани во внутренних точках промежутка $I$.

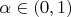
Пусть $x^*$ точка, в которой достигается верхняя грань и $x^*$ внутренняя точка. Если $f$ не константа, то существует $a$ такая, что $f(a)<f(x^*)$. Выберем точку $b$ по другую сторону относительно $x^*$, т.е. $x^*\in(min(a,b),max(a,b))$. Тогда существует $\alpha\in(0,1)$ такое, что имеет место равенство $x^*=\alpha a+(1-\alpha)b$. Из условия выпуклости получаем $f(x^*)\le\alpha f(a)+(1-\alpha)f(b)<f(x^*)$. Противоречие.

Цитата:

3) что если $I= \mathbb{R}$ и $f$ не равна постоянной, то $f$ не ограничена на $I$.

Из условия выпуклости для точек $a<b<b+(b-a)n,n\in\mathbb{N}$ получаем $f(b)=f(\frac{n}{n+1}a+\frac{1}{n+1}(b+(b-a)n))\le\frac{n}{n+1}f(a)+\frac{1}{n+1}f(b+(b-a)n)$. Откуда $(n+1)f(b)-nf(a)\le f(b+(b-a)n)$ или $f(b+(b-a)n)\ge f(b)+n(f(b)-f(a))$. Если $f(b)>f(a)$, то неограниченность очевидна. В случае монотонно убывающей рассмотрим $\hat f(x)=f(-x)$.

[трапезун]

Сергей Михайлов писал(а):

что такое "множество относительно компактно"?

Множество $I$ в топологическом пространстве $\mathbb{R}$ называется относительно компактным, если $I$ содержится в компактном множестве.

[трапезун]

Пытаюсь решить задачу 2 в несколько упрощённом варианте.
Пусть функция $f$ строго выпукла, непрерывна и строго убывает на $(a, b)$,
где $a$ и $b$ - конечные числа. Доказать, что $f$ ограничена снизу на $(a, b)$.

Очевидно в силу непрерывности и строго убывания $f$ имеем, что
$ \inf \{ f(x), x \in (a, b) \} = f(b-0)$. Остаётся показать, что $f(b-0)$ - конечное число. Никак не получается это сделать.

[nworm]

Проведём прямую через две точки кривой. Пусть $(b,y)$ - точка пересечения проведённой прямой и прямой $x=b$. Тогда неравенство $f(b-0)<y$ противоречит строгой выпуклости $f$.