При прохождении плоскополяризованного луча через полуволновую пластинку, поворачивается плоскость поляризации, как на картинке:
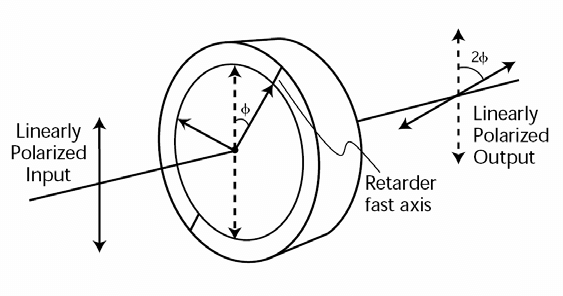
Этот эффект можно интерпретировать как изменение частоты луча с круговой поляризацией, при вращении пластинки, ведь плоскую поляризацию можно разложить на две круговых поляризации. Такое изменение частоты изменяет разницу фаз в базисе круговых поляризаций и поворачивает плоскость поляризации входящего луча на выходе. Так должно быть по
эффекту Садовского, ведь луч с круговой поляризацией меняет свою поляризацию на противоположную, при прохождении через полуволновую пластину, следовательно, передает момент импульса пластинке, и должен изменять свою частоту, если пластина вращается, по закону сохранения энергии. Такое изменение частоты было зафиксировано экспериментально.
Теперь рассмотрим отражение луча с круговой поляризацией. Например, от блестящей сферы. При отражении меняется проекция момента импульса луча на вектор падения, поэтому тут тоже должен быть эффект Садовского. Но ведь здесь нет поворота поляризации отраженного плоскополяризованного луча при повороте сферы! Если нет этого эффекта, то нет и изменения частоты отраженного луча с круговой поляризацией. Как такое может быть?
Еще один пример. Пусть у нас есть диск из стопки стеклянных пластин, на который падает луч с круговой поляризацией под углом Брюстера, как на картинке:

Луч с круговой поляризацией расщепляется на два плоскополярованых луча, вертикальна проекция момента импульса луча уменьшается до нуля, после прохождения поляризатора, поэтому должен наблюдаться эффект Садовского. Предположим, что так и есть, тогда, при вращении стопы Столетова вокруг вертикальной оси, должна изменяться частота отраженных и прошедших лучей с плоской поляризацией. Но ведь падающий луч с плоской поляризацией не имеет момента импульса, поэтому и плоскополяризованный луч, на выходе из поляризатора в виде вращающейся стопки Столетова, не может изменить свою частоту. И его гипотетическое изменение частоты при падение луча с круговой поляризацией противоречит линейности уравнений Максвелла.
Таким образом возникает вопрос - а существует ли вообще эффект Садовского при отражение? Возможно, при отражение момент импульса отраженного луча не изменяется? Потому что только так можно решить вышеизложенные противоречия.
Спасибо тем, кто может развеять эти сомнения.