До сих пор мы рассматривали случаи, когда предельным распределения для арифметической функции являлось нормальное распределение.
Сейчас мы рассмотрим, в том числе, и другие случаи предельного распределения арифметических функций и докажем несколько утверждений для указанных случаев.
Можно начать обсуждение прямо с этого сообщения. Готов ответить на вопросы.
Начнем рассмотрение с сильно аддитивных арифметических функций. В отношении данных функций Кубилюс доказал теоремы.
Теорема 4.1 (Кубилюс)
Для того, чтобы законы распределения

, где

- сильно аддитивная арифметическая функция класса

, сходились к предельному с дисперсией равной 1, необходимо и достаточно, чтобы существовала такая неубывающая функция

с вариацией равной 1, чтобы при

во всех точках непрерывности

выполнялось условие:

где соответственно

- среднее значение и дисперсия

, а

- функция Колмогорова:


где

- постоянные

.
Возникает вопрос, какие законы вообще могут выступать в качестве предельных в теореме 4.1? На этот вопрос дает ответ следующая теорема.
Теорема 4.3 (Кубилюс)
Класс предельных законов, к которым стремится закон распределения

с дисперсией равной 1 для сильно аддитивной арифметической функции

, принадлежащей классу

, совпадает с классом законов

.
Как я писал ранее, что если существует предельное распределение сильно аддитивной арифметической функции, то оно совпадает с предельным распределением суммы асимптотически независимых случайных величин и в этом случае данная арифметическая функция относится к классу

.
Известно (Кубик), что предельное распределение суммы асимптотически независимых случайных величин, принимающих два значения, при определенных условиях, которые мы рассмотрим далее подробно, совпадает с одним из законов распределения

.
Отсюда следует, что если существует предельное распределение сильно аддитивной арифметической функции, то оно совпадает с одним из законов распределения

.
Таким образом, справедливо следующее утверждение.
Утверждение 1.1
Пусть существует сильно аддитивная арифметическая функция

, для которой ряд

- расходится.
Обозначим

, тогда, если

при

, где

- функция Колмогорова и

, то:
1.Можно построить случайную величину, являющуюся суммой независимых случайных величин, принимающих два значения, имеющую такое же предельное распределение, как

при

, для которой асимптотики среднего значения и дисперсии соответственно равны:

.
2.Асимптотика центрального момента

-ого порядка для

при

определяется по формуле:

Доказательство
Так как выполняются условия теоремы 4.1 (

при

, где

- функция Колмогорова), то на основании теоремы 4.1 законы распределения

, где

- сильно аддитивная арифметическая функция класса

, сходятся к предельному с дисперсией равной 1. На основании теоремы 4.3 класс этих предельных законов совпадает с

.
С другой стороны, так как ряд

- расходится и поэтому

, и на основании леммы 4.6 (Кубика) существует последовательность независимых случайных величин, принимающих не более двух значений -

, для которой закон распределения

, при условии

, сходится к предельному, совпадающему с

.
Давайте построим такую последовательность независимых случайных величин

и покажем, что для нее будет выполняться условие

.
Построим данную случайную величину. Пусть случайная величина

принимает два значения:

с вероятностью

и

с вероятностью

.
Тогда среднее значение и дисперсия

соответственно равны:
![$E[X_p]=f(p)/p,D[X_p]=f^2(p)/p$ $E[X_p]=f(p)/p,D[X_p]=f^2(p)/p$](https://dxdy-04.korotkov.co.uk/f/3/2/a/32adf84d5aa78349360da17c334c61b382.png)
.
Так как

, то учитывая, что

, получим, что выполняется

.
Определим случайную величину

, где

- независимые случайные величины. Тогда среднее значение и дисперсия
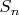
соответственно равны:
![$E[S_n]=\sum_{p \leq n} \frac {f(p)}{p}, D[S_n]=\sum_{p \leq n} \frac {f^2(p)}{p}$ $E[S_n]=\sum_{p \leq n} \frac {f(p)}{p}, D[S_n]=\sum_{p \leq n} \frac {f^2(p)}{p}$](https://dxdy-04.korotkov.co.uk/f/7/f/8/7f806017aa622b96ae59fafdf829721482.png)
т.е. равны асимптотикам соответственно среднего значения и дисперсии

при

. Таким образом, совпадают предельные распределения

и
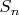
при

.
Следовательно мы доказали первую часть утверждения. Теперь докажем вторую часть. Так как совпадают предельные распределения

и
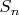
при

, то совпадают и центральные моменты всех порядков. Поэтому достаточно определить центральные моменты у случайной величины
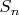
.
Сначала определим центральный момент

-ого порядка для

:
![$E[(X_p-\frac{f (p)} {p})^k]=E[X_p]^k - kE[X_p^{k-1}\frac{f (p)} {p}] + \frac{k(k-1)}{2}E[X_p^{k-2}\frac{f ^2(p)} {p}]-...+(-1)^k\frac{f^k (p)} {p}=\frac{f^k (p)} {p}-k\frac{f^{k-1}(p)}{p}\frac{f (p)} {p} +\frac{k(k-1)}{2}\frac{f^{k-2}(p)}{p}\frac{f^2 (p)} {p^2}+...(-1)^k\frac{f^k (p)} {p^k}$ $E[(X_p-\frac{f (p)} {p})^k]=E[X_p]^k - kE[X_p^{k-1}\frac{f (p)} {p}] + \frac{k(k-1)}{2}E[X_p^{k-2}\frac{f ^2(p)} {p}]-...+(-1)^k\frac{f^k (p)} {p}=\frac{f^k (p)} {p}-k\frac{f^{k-1}(p)}{p}\frac{f (p)} {p} +\frac{k(k-1)}{2}\frac{f^{k-2}(p)}{p}\frac{f^2 (p)} {p^2}+...(-1)^k\frac{f^k (p)} {p^k}$](https://dxdy-04.korotkov.co.uk/f/3/3/9/339fc197e4e8006e1a0b1480e315e5f682.png)
.
Таким образом, центральный момент

-ого порядка для

равен:
![$E[(X_p-\frac{f (p)} {p})^k]=\frac{f^k (p)} {p}+O(\frac{f^k (p)} {p^2})$ $E[(X_p-\frac{f (p)} {p})^k]=\frac{f^k (p)} {p}+O(\frac{f^k (p)} {p^2})$](https://dxdy-01.korotkov.co.uk/f/0/7/c/07cdfaba71cc0393985a4fd70baa980882.png)
.
Получаем,что центральный момент

-ого порядка для
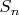
:
![$E[S^k,n]=\sum_{p \leq n} \frac {f^k(p)}{p}+O(\sum_{p \leq n}\frac{f^k (p)} {p^2})=\sum_{p \leq n} \frac {f^k(p)}{p}+o(\sum_{p \leq n}\frac{f^k (p)} {p})$ $E[S^k,n]=\sum_{p \leq n} \frac {f^k(p)}{p}+O(\sum_{p \leq n}\frac{f^k (p)} {p^2})=\sum_{p \leq n} \frac {f^k(p)}{p}+o(\sum_{p \leq n}\frac{f^k (p)} {p})$](https://dxdy-01.korotkov.co.uk/f/0/a/7/0a7d2113d9d8b37737657047ee64bb1182.png)
, т.е.
![$E[S^k,n] \sim \sum_{p \leq n} \frac {f^k(p)}{p}.$ $E[S^k,n] \sim \sum_{p \leq n} \frac {f^k(p)}{p}.$](https://dxdy-03.korotkov.co.uk/f/e/2/9/e29529fa98324368591b373acdd3ea8282.png)
Следовательно, мы доказали вторую часть утверждения.
Рассмотрим случаи, когда выполняется условие

.
Если

, то

, поэтому в этом случае выполняется условие

.
Если

, то в этом случае также выполняется условие

.
Напомню, что в этих случаях сильно аддитивная арифметическая функция

при

имеет предельным нормальное распределение.
В качестве примера на использование утверждения 1.1 приведем сильно аддитивную арифметическую функцию, имеющую предельным распределением, как доказал Кубилюс, функцию

:

, если

;

, если

;

, если

,
где

- классы простых чисел

.
Число простых чисел

асимптотически равно:

,
если

не равно нулю.
Число простых чисел

асимптотически равно:

,
если

не равно нулю.
Если же

или

, то

и

- пусты.
Число простых чисел

асимптотически равно:

.
Используя результаты темы "Асимптотика сумматорных функций простого аргумента", получим асимптотику центрального момента

- ого порядка для данной сильно аддитивной арифметической функции:

,

,

.
Таким образом, получим:

.
Проверим выполнение в этом примере условия:

.

, т.е. стремится к нулю при

.