Spatial indipendence. MRI signal

[Anton_74]

Magnetic Resonance Imaging Physical Principles and Sequence Design Second Edition By Robert W. Brown et. all © 2014 byJohn Wiley & Sons,Inc
Problem 7.4

Цитата:

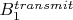
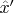
Consider a $\pi/2$-pulse produced by a left-circular $B^{transmit}_{1}$ field lying along $\hat{x}'$ in
the rotating frame. It results in the rotation of the equilibrium magnetization of a
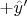
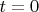
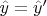
sample into the $+\hat{y}'$ direction at $ t = 0 $ (at which time $\hat{y} = \hat{y}'$ ). (The magnetization
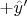
would subsequently precess such that it remains pointed along the $+\hat{y}'$ direction in the rotating frame.)

a) Find the phase angle $\varphi_0$ in (7.22) corresponding to this initial condition.
b) Find $\varphi_0$ for the imaging scenario where the $\pi/2$-pulse is produced by $B^{transmit}_{1}$
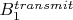
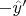
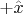
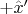
along $-\hat{y}'$ (so that the magnetization is rotated into $+\hat{x}$ at $t = 0$ and remains pointed along the $+\hat{x}'$ direction in the rotating frame thereafter).
c) Repeat (b) for B1 along $\hat{y}'$.
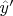
d) Repeat (b) for Btransmit along $-\hat{x}'$.

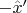
Сигнал получаемы от одного вокселя апроксимируется так:

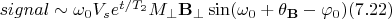
$signal \sim \omega_0 V_s e^{t/T_2} M_\perp \mathbf{B}_\perp \sin (\omega_0 + \theta_\mathbf{B} -\varphi_0) (7.22)$ (space-independent limit)

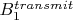
Динамика вектора намагниченности мне понятна: если прикладывать магнитное поле во вращающей ск (вск), то после применения $B^{transmit}_1$ вектор будет находится в плоскости $x'-y'$.

Урванение движения в лск (лабороторной ск) имеют вид описанный в формулах (4.25)-(4.27):
$ M_x(t) = e^{-t/T_2} (M_x(0) \cos\omega_0 t + M_y(0) \sin \omega_0 t) (4.25) \\ M_y(t) = e^{-t/T_2} (M_y(0) \cos\omega_0 t - M_x(0) \sin \omega_0 t) (4.26) \\ M_z(t) = M_z(0) e^{-t/T_1} + M_0 (1-e^{-t/T_1}) (4.27) $

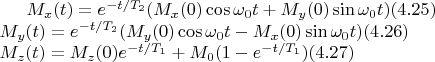
Подскажите как подойти к этой задаче?

[svv]

Из (4.29) и (4.31) в момент $t=0$ получаем:
$M_x(0)+iM_y(0)=M_\perp(0)e^{i\varphi_0}\,,$
где $M_\perp(0)$ — модуль поперечной составляющей намагниченности, вещественное положительное число.

В a) надо лишь понять, какое $\varphi_0$ взять в правой части, чтобы в левой получилось $M_x(0)=0, \;M_y(0)>0$.
В b) аналогично, но надо обеспечить $M_x(0)>0, \;M_y(0)=0$.
В c) и d) чуть сложнее, тут дано не начальное направление поперечной намагниченности, а направление создающего её магнитного поля.

[Anton_74]

svv в сообщении #1509833 писал(а):

Из (4.29) и (4.31) в момент $t=0$ получаем:
$M_x(0)+iM_y(0)=M_\perp(0)e^{i\varphi_0}\,,$
где $M_\perp(0)$ — модуль поперечной составляющей намагниченности, вещественное положительное число.

В a) надо лишь понять, какое $\varphi_0$ взять в правой части, чтобы в левой получилось $M_x(0)=0, \;M_y(0)>0$.
В b) аналогично, но надо обеспечить $M_x(0)>0, \;M_y(0)=0$.
В c) и d) чуть сложнее, тут дано не начальное направление поперечной намагниченности, а направление создающего её магнитного поля.

Спасибо, я думал об этом, но как-то не срослось, что комплексные числа тоже отображают точки на плоскости, как и вектор намагниченности в поперечной плоскости.

В разделе 2.3.2 дается описания направления вращения вектора намагниченности - используется правило правило левой руки (противоположное правилу буравчика для правой руки).
Это нагляднее продемонстрировано в разделе 3.3.1.

Тогда становится не сложным определить направление вектора намагниченности в момент времени $t=0$.