Формальная и метатеория

[maximav]

Someone писал:
"... формальная теория может сказать что-либо только о своих объектах (в данном случае — о множествах), а её формулы её объектами не являются, а во-вторых, понятие истинности в формальной теории начисто отсутствует. Однако у нас есть метатеория, которая использовалась для формулировки ...''

Не могли бы вы прокомментировать это место подробнее? (для даунов, или ссылку где на форуме). Возьмем, например, в качестве формальной теории, группы/алгебры. Что здесь является формулами, которые "её [теории] объектами не являются"? И, возьмем теперь, скажем, некатегоричность аксиом этой теории. Это утверждение явно из разряда метатеорем для нее. Хотелось бы снять путаницу, хотя бы на этом примере (или на ZFC), "кто и что" в этих теориях является формулами, объектами, правилами вывода, утверждением об истинности и т.д.? Заранее спасибо.

[arseniiv]

Проще взять элементарную теорию групп, потому что алгебры потребуют по-хорошему или двусортную логику, или принятие кольца/поля скаляров алгебры как «внешнего» понятия, которое аксиомы не стремятся определить, а используют как есть, — и и то, и то обычно почему-то требует много дополнительных объяснений.

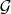
Элементарная теория групп в одном из изложений — это теория над языком $\mathcal G$ с символами ${*}, e, {}^{-1}$ (их местность и тип определим контекстом использования) и аксиомами
(G1) $\forall x. \; \forall y. \; \forall z. \; (x * y) * z = x * (y * z)$;
(G2) $\forall x. \; x * e = x \wedge e * x = x$;
(G3) $\forall x. \; x * x^{-1} = e \wedge x^{-1} * x = e$.

В этой элементарной теории мы говорим только об элементах одной группы и можем сказать довольно мало, так что это совершенно далеко не вся теория групп в обычном понимании; её даже стоит называть «теорией группы».

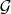
Что такое формулы языка $\mathcal G$, аксиоматическая теория (т. е. весь аппарат выводимости), логические следствия формул, интерпретации языка и модели теории, определяются очевидно вне этой маленькой теории. И чтобы назвать, «где» они определяются, и говорят «метатеория». Она может быть произвольной и обычно это какая-то неформальная теория (потому что рассматривать башни из нескольких теорий, определяемых внутри друг друга, нужно лишь в специфических случаях, которые я даже не помню). Чем конкретно будут являться все эти вещи, зависит от этой теории. Если мы примем предположение, что это какая-то неформальная теория множеств, то мы получим один из возможных вариантов определений, но мы можем придерживаться какой-нибудь конструктивной теории, где есть какой-то набор первичных неопределяемых символов или, возможно, любой интересующий нас не более чем счётный набор таких символов, которые мы вольны вводить в любых количествах посередине развития, соблюдая лишь некоторые естественные ограничения. И чем конкретно всё это будет, в любом случае вам придётся узнавать из учебника матлогики, доходящего до теорий первого порядка, потому что переписывать сюда кучу определений из учебника мало кто захочет.

А если вы имели в виду теорию пошире элементарной теории группы, которая представлена выше, то всё будет немного хуже, потому что в таком случае обычно уже не определяют отдельную теорию, а выражают всё нужное в терминах какой-то достаточно разнообразной теории типа теории множеств. Вот тогда её имеет смысл рассматривать формальную, чтобы что-то о ней устанавливать, но работающий в теории групп математик этого делать должен не будет, она будет для него большей частью неформальной и оставаться на том же уровне, на каком рассматриваемая им теория групп (потому что её нельзя будет никак рассоединить от теории множеств, когда группа сама по себе множество, рассматриваемое вместе с бинарной операцией, или набором операций в духе аксиоматики выше, и когда теоремы о группах — это теоремы теории множеств, просто говорящие в основном о группах, а не о произвольных множествах).

-- Чт мар 11, 2021 22:44:25 --

Связь тут такая, что теория выше — это просто-напросто определение группы, как вообще по смыслу, так и с точки зрения теории групп, вложенной в теорию множеств (или в другую теорию-основание) — мы говорим, что множество с некоторыми операциями — это группа, если они являются моделью соответствующих аксиом. Покуда таких аксиом приемлемое количество (например конечное как тут), это всё транслируется в одну толстую такую формулу-определение в языке теории множеств (или другой теории-основания), имеющей вид

$$\textrm{группа}(G, {*}, e, {}^{-1}) \Longleftrightarrow ({*}\colon G^2 \to G) \wedge (e \in G) \wedge ({}^{-1}\colon G \to G) \wedge \mathrm{G1}' \wedge \mathrm{G2}' \wedge \mathrm{G3}',$$

где G1′, …, G3′ — формулы G1, …, G3, в которых мы сделали все кванторы ограниченными $G$.

-- Чт мар 11, 2021 22:46:06 --

(И эта связь по-моему довольно очевидна(?). Её нигде не прописывали явно на моей памяти, что не мешало ей автоматически прийти лично мне в голову при первых столкновениях с формальными теориями.)

[Someone]

maximav в сообщении #1508698 писал(а):

Возьмем, например, в качестве формальной теории, группы/алгебры. Что здесь является формулами, которые "её [теории] объектами не являются"?

Грубо говоря, формулы и термы — это то, что Вы пишете на бумаге. При этом термы — имена объектов, а формулы — утверждения об этих объектах. Если ваша теория — это теория групп, то, например, $a,b,c$ могут быть именами каких-то элементов группы, а формула $a\circ b=c$ тогда будет некоторым утверждением об этих объектах (заметим, что $a\circ b$ также является термом, то есть, именем некоторого объекта). Я просто утверждаю, таким образом, что запись "$a\circ b=c$" не является элементом группы. Является ли формула $a\circ b=c$ ложной или истинной, сказать нельзя, пока у нас нет никакой интерпретации нашей теории. Чтобы получить интерпретацию, мы должны каждому терму сопоставить некоторый объект, а символу "$\circ$" — некоторую бинарную операцию (функцию двух переменных). Кроме термов и функций, формула может содержать отношения (предикаты; в рассмотренной формуле предикатом является "$=$"), кванторы, логические связки, скобки. Константы также являются термами; иногда константы рассматривают как нульарные операции или функции.

Подробнее смотрите в учебнике математической логики. Изложить всё здесь совершенно не реально.