|
gris |
некоторое свойство многогранников  06.03.2021, 09:35 |
|
| Заслуженный участник |
 |
13/08/08
14496
|
|
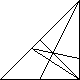
Есть довольно известная задача: доказать, что в выпуклом многограннике найдутся две грани с одинаковым количеством сторон. Она легко решается через Принцип Дирихле по отношению к грани с максимальным количеством сторон. А вот если многогранник не выпукл? Говорят, что утверждение верно. Я придумал "контрпример": плоский пятиугольник с диагональю. Он сам одна грань, две части — две другие грани: треугольник и четырёхугольник. Но является ли он многогранником? По некоторым определениям является.
Нет ли советов?
|
|
|
|
 |
|
arseniiv |
Re: некоторое свойство многогранников  06.03.2021, 16:05 |
|
| Заслуженный участник |
 |
27/04/09
28128
|
|
Это вы сделали объём многогранника нулевым, а можно ли всё как-нибудь гиперболизировать и сделать его отрицательным? Там наверно будет яснее, должно это выполняться (и стоит ли навешивать дополнительные условия чтоб стало) или нет.
|
|
|
|
 |
|
gris |
Re: некоторое свойство многогранников  06.03.2021, 20:25 |
|
| Заслуженный участник |
 |
13/08/08
14496
|
|
мне кажется, что задача и в расширенной постановке для невыпуклых многогранников достаточно известна и имеет несложное решение. Но никак не могу его отыскать или придумать. Для повторения ПД нужно показать, что количество граней в многограннике не меньше числа сторон у грани с наибольшим их количеством (ну минус два). Для выпуклых многогранников, у которых и все грани выпуклы, это очевидно. У каждой грани количество смежных граней равно числу её сторон. Но для невыпуклых это не верно. Пример тоже очевиден.
|
|
|
|
 |
  |
Страница 1 из 1
|
[ Сообщений: 3 ] |
|
Модераторы: Модераторы Математики, Супермодераторы



