Я не знаю, в какую сторону смотреть, но есть несколько замечаний.
1) Если

— квадрат нормы функции

, то эта штука уже подразумевает интегрирование по

.
2) Вместо

, скорее всего, должно быть

.
3) Если

действительно сферические координаты, их лучше обозначить стандартно:

.
4) Причём угол

меняется только в диапазоне
![$[0,\pi]$ $[0,\pi]$](https://dxdy-03.korotkov.co.uk/f/2/3/8/2385bc03c71e0b4fd8db3bac2e36c7f282.png)
.
5) И подинтегральная функция должна содержать ещё якобиан

.
6) Бесконечность

«не пропечаталась» в верхнем пределе интеграла по

, потому что вместо
\infty набрано
\intfy.
7) Конструкция интеграла намекает, что Вы ищете такой «поворот функции

вокруг центра», после которого

наилучшим образом совпадёт с

. Но

описывает не поворот, а что-то совсем другое. Для простоты возьмите

. Сдвиг точек на

вдоль меридианов — это не поворот. А вот сдвиг вдоль параллелей на
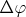
— это поворот.



