Проверка ГОСТа статистическим моделированием

[Александрович]

Существует ГОСТ Р ИСО 16269-8-2005 Статистические методы. Статистическое представление данных. Определение предикционных интервалов. Далее из него.

Термины и определения - предикционный интервал (predication interval): Диапазон значений переменной, полученный по случайной выборке из непрерывной совокупности, для которого можно утверждать с заданным уровнем доверия, что не менее чем заданное количество значений в будущей случайной выборке из той же самой совокупности попадает в этот интервал.

Предикционные интервалы для нормальной совокупности с неизвестным стандартным отклонением. Односторонние интервалы.

Односторонний предикционный интервал для нормальной совокупности с неизвестным стандартным отклонением имеет вид $( -\infty , \overline{x} + ks)$ или $( \overline{x} + ks, \infty )$, где \overline{x} - выборочное среднее; $s$ - выборочное стандартное отклонение; $n$- объем выборки. Коэффициент предикционного интервала $k$ зависит от $n$, от объема будущей выборки $m$ и от уровня доверия $C$. Значения $k$ представлены в таблицах приложения А.

В таблице для $n=10$, $m=300$ и $C=90$%, $k=4,4306$.

Сгенерировал нормально распределённую $N(0;1)$ будущую выборку объёмом $m=300$из неё получил $291$ выборку объёмами по $n=10$ и 1-ую и 300-ую порядковую статистики $x_{300}$и$x_1$. Для каждой из $291$ выборки объёмом по $n=10$ определил \overline{x}, $s$ и $k$ по формулам:

$k_1=\frac{x_{300}-\overline{x}}{s}$; $k_2=\frac{\overline{x}-x_{1}}{s}$.

Выборок объёмом по $m=300$ нагенерировал $1000$ штук и для каждой нашёл $k_1$ и $k_2$. Все их поместил в один массив и определил в нём $90$%-ный персентиль. Он оказался выше, чем найденный по таблице: $4,4768 $ против $4,4306$. Причём это наблюдается на всех уровнях доверия и чем выше, тем завышение больше. Например при $C=99,9$% $k=11,8758$ против $k=8,8082$.

Что же я делаю неправильно?

[Xaositect]

Александрович в сообщении #1507473 писал(а):

Сгенерировал нормально распределённую $N(0;1)$ будущую выборку объёмом $m=300$из неё получил $291$ выборку объёмами по $n=10$ и 1-ую и 300-ую порядковую статистики $x_{300}$и$x_1$.

Тут у Вас все зависимо совершенно неочевидным образом. Генерируйте независимые выборки и считайте $\frac{\bar{x}-y_1}{s_x}$.

Также в той копии стандарта, которую я смог найти, в таблице не нашел $m = 300$. Для $m=250$ у меня значения совпадают (в пределах разброса: генерировал 10000 раз по 10000 выборок, для 90% дает только 2 знака $k$).

[Александрович]

Xaositect в сообщении #1507518 писал(а):

в таблице не нашел $m=300$.

Коэффициент для $m=300$ находил линейной интерполяцией по $m=250$ и $m=500$.

[Александрович]

Xaositect в сообщении #1507518 писал(а):

Тут у Вас все зависимо совершенно неочевидным образом. Генерируйте независимые выборки и считайте

Сделал так. Всё равно систематическое завышение остаётся.
Для $90$% $4,4719$ против $4,4306$, для $99,9$% $12,1930$ против $8,8082$.

[Xaositect]

> for (j in 1:10000) { for (i in 1:10000) { x <- rnorm(10); y <- rnorm(300); k[i] = (mean(x) - min(y))/sd(x) }; k = sort(k); c[j,1:6] = c(k[9000], k[9500], k[9750], k[9900], k[9950], k[9990]) }
> summary(c[1:1000, 1])
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  4.370   4.433   4.450   4.450   4.468   4.540 
> summary(c[1:1000, 6])
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  7.868   8.543   8.760   8.782   8.996  10.119 

Малые отклонения я склонен объяснять неточностью линейной интерполяции.

-- Ср мар 03, 2021 10:17:39 --

Вы сколько раз генерируете для 99.9%? Если несколько тысяч, то это явно недостаточно (по-хорошему, и моих 10 000 недостаточно, всего-то 10 порядковая статистика с краю)

[Александрович]

Проверяю свой ГСЧ. Думаю он смещён в область больших значений.

-- Ср мар 03, 2021 16:47:57 --

Xaositect в сообщении #1507608 писал(а):

Вы сколько раз генерируете для 99.9%?

Позорно мало.

[Александрович]

Xaositect, спасибо большое за то, что не поленились сделать аналогичное моделирование.
Подправил свой ГСЧ и все получилось!

(Оффтоп)

Было
0,9 4,413 0,95 5,055 0,975 5,714 0,99 6,705 0,995 7,646 0,999 11,133
250 4,372 4,957 5,553 6,375 7,032 8,706

отн. 1,009 1,020 1,029 1,052 1,087 1,279

стало
0,9 4,390 0,95 4,942 0,975 5,590 0,99 6,457 0,995 7,117 0,999 8,915
250 4,372 4,957 5,553 6,375 7,032 8,706

отн. 1,004 0,997 1,007 1,013 1,012 1,024

Для любого уровня доверия для нахождения $k$ брал $10000$ шт. значений.

[Александрович]

Продолжаю далее по ГОСТу.

Цитата:

Приложение Н (справочное). Статистическая теория, используемая при составлении таблиц

Н.1 Односторонние предикционные интервалы для нормальной совокупности с неизвестным стандартным отклонением совокупности (приложение А)
Н.1.1 Данные

Случайная выборка из $n$ наблюдений $x_1, x_2, ... , x_n$ принадлежит нормальной совокупности с неизвестным средним $\mu$ и неизвестным стандартным отклонением $\sigma$ . Выборочное среднее и выборочное стандартное отклонение - это $\bar{x}$ , $s$ .

Н.1.2 Задача

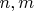
Для заданных значений $n, m$ и $\alpha$ необходимо определить минимальное значение коэффициента $k$ , для которого можно утверждать с уровнем доверия не менее $100(1- \alpha)$%, что ни одно из $m$ будущих наблюдений не превысит значения $\bar{x}+ks$ . Из соображений симметрии, это значение $k$ соответствует утверждению, что ни одно из $m$ будущих наблюдений не будет меньше $\bar{x}-ks$ с уровнем доверия $100(1- \alpha)$%.

Н.1.3 Решение задачи для конечного $n$

Коэффициент предикционного интервала - минимальное значение $k$, удовлетворяющее неравенству

$\int\limits_{0}^{\infty} g(s)\int\limits_{-\infty}^{\infty}\Phi^m(\bar{x}+ks)f(\bar{x})d\bar{x}ds \geqslant 1-\alpha$, (Н.1)

где $f(\bar{x})$ и $g(s)$ - соответственно плотности распределения выборочного среднего и выборочного стандартного отклонения для выборки из стандартного нормального распределения, а $\Phi(\bullet)$ является функцией этого распределения, т.е.

$f(\bar{x})=\sqrt{\frac{n}{2\pi}}\exp(-\frac{n}{2}\bar{x}^2), -\infty< \bar{x}<\infty$,

$g(s)=\frac{\nu^{\nu/2}s^{\nu-1}}{2^{(\nu/2)-1}\Gamma(\frac{\nu}{2})} \exp(-\nu^{-\nu^2/2})$, $\, s\geqslant0$.

$\Phi(t)=\int\limits_{-\infty}^{t}\frac{1}{\sqrt 2\pi}\exp(-\frac{1}{2}u^2)du$,

$\Gamma(\frac{\nu}{2})=\int\limits_{0}^{\infty} x^{\frac{\nu}{2}-2} \exp(-x)dx$,

где $\nu=n-1$.

Для каждой заданной комбинации значений $n ,\; m$ и $\alpha$ значение, представленное в таблицах приложения А, является минимальным значением $k$ (с точностью до третьего десятичного знака), удовлетворяющим неравенству (Н.1).

Н.1.4 Решение задачи для бесконечного $n$
При $n$ , стремящемся к бесконечности, (Н.1) стремится к неравенству

$\Phi(k)\geqslant 1-\alpha$. (Н.2)

Неравенство (Н.2) имеет решение

$k\geqslant \Phi^{-1} [(1-\alpha)^{\frac{1}{m}}]$. (Н.3)

Минимальные значения $k$ (с тремя десятичными знаками), удовлетворяющие неравенству (Н.3), приведены в последних строках таблицы приложения А.

1. Помогите понять второе подынтегральное выражение в формуле (Н.1). В ней $\Phi^m(\bar{x}+ks)$ - это функция распределения крайней порядковой статистики $\bar{x}+ks$. Для чего её умножают на функцию плотности распределения $f(\bar{x})$ ?

[Xaositect]

Пусть $X$ - первая выборка, $Y$ - вторая выборка, $\bar{X} = \frac{\sum X_k}{n}$, $S = \sqrt{\frac{(X_k - \bar{X})^2}{n-1}}$, $Y_{(m)} = \max \{Y_1, \dots, Y_m\}$.
Для фиксированных значений $\bar{X} = \bar{x}$ и $S = s$ условная вероятность $\mathbb{P}(Y_{(m)} \leq \bar{X} + kS \mid \bar{X} = \bar{x}, S = s) = \mathbb{P}(Y_{(m)} \leq \bar{x} + ks) = \Phi^m (\bar{x} + ks)$.
Для того, чтобы найти полную вероятность, мы интегрируем по всем возможным $\bar{x}, s$ и получаем $\mathbb{P}(Y_{(m)} \leq \bar{X} + kS) = \iint \mathbb{P}(Y_{(m)} \leq \bar{X} + kS \mid \bar{X} = \bar{x}, S = s) f(\bar{x}) g(s) d\bar{x} ds$ $= \iint \Phi^m(\bar{x} + ks) f(\bar{x}) g(s) d\bar{x} ds$

[Александрович]

Xaositect, спасибо. То есть берётся сумма произведений троек всевозможных вероятностей.

[Александрович]

Теперь ещё такой вопрос. Пусть нам точно известны параметры нормального распределения $\mu$ и $\sigma$. И нам нужно узнать, чему будет равняться крайняя порядковая $250$-ая статистика в выборке из этой ГС с уровнем доверия $90$%? Это делается без извлечения пробной выборки из той же ГС.

$\Phi^{-1}(0,9^{\frac{1}{250}})\approx 3,338 $ (1)

и $x_{250}\approx \mu + 3,338\, \sigma$ (2)

Если параметры нормального распределения находятся по выборке объемом $10$, то

$\tilde{x}_{250}\approx \bar{x} + 4,372 \,s$ (3)

Отметим при этом, что

$\Phi(4,372;0;1)\approx 0,99999384 $ (4)

Пусть теперь ГС имеет распределение Вейбулла-Гнеденко $F(x)$ с неизвестными параметрами $\alpha$ и $\beta$. По случайной выборке объёмом $10$ определим выборочные параметры этого распределения $\tilde{\alpha},\, \tilde{\beta}$.

Получаем значение для $\tilde{x}_{250}\approx \tilde{\beta} \sqrt[\alpha]{-\ln(1-F(\tilde{x}_{250}))}$.

Теперь вопрос. Правомочно ли будет, если я вместо $F(\tilde{x}_{250})$ подставлю значение вероятности из формулы (4)?