Пусть
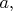

,

и

неотрицательные числа, для которых

. Докажите, что:...
Скорее всего верно следующее:
Определим многочлены

и

из разложения
![$2^{n-1}t^{\left[\frac{n+1}{2}\right]}P_{n}(t)+2^{n-1}t^{\left[\frac{n}{2}\right]}Q_{n}(t)\sqrt{t(t+4)} = \left(t+\sqrt{t(t+4)}\right)^n,$ $2^{n-1}t^{\left[\frac{n+1}{2}\right]}P_{n}(t)+2^{n-1}t^{\left[\frac{n}{2}\right]}Q_{n}(t)\sqrt{t(t+4)} = \left(t+\sqrt{t(t+4)}\right)^n,$](https://dxdy-04.korotkov.co.uk/f/7/6/8/7688c5d0e54191925fd55c511825010c82.png)
тогда для неотрицательных

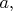


и

для которых

выполняется:
____

![$$\sqrt[m]{\frac{a}{b+k}}+\sqrt[m]{\frac{b}{c+k}}+\sqrt[m]{\frac{c}{d+k}}+\sqrt[m]{\frac{d}{a+k}}\leq\begin{cases}
2(\gamma+2)\sqrt[m]{\frac{P_{2n-1}(\gamma)}{P_{2n+1}(\gamma)}},\quad S\geqslant 2k(2n-1)\\
4\sqrt[m]{\frac{S}{S+4k}},\quad S\leqslant k(2n-1)
\end{cases}$$ $$\sqrt[m]{\frac{a}{b+k}}+\sqrt[m]{\frac{b}{c+k}}+\sqrt[m]{\frac{c}{d+k}}+\sqrt[m]{\frac{d}{a+k}}\leq\begin{cases}
2(\gamma+2)\sqrt[m]{\frac{P_{2n-1}(\gamma)}{P_{2n+1}(\gamma)}},\quad S\geqslant 2k(2n-1)\\
4\sqrt[m]{\frac{S}{S+4k}},\quad S\leqslant k(2n-1)
\end{cases}$$](https://dxdy-03.korotkov.co.uk/f/a/3/8/a387a72ac0b7640ed62f96da2521c61e82.png)
где

- неотрицательный корень уравнения

____

![$$\sqrt[m]{\frac{a}{b+k}}+\sqrt[m]{\frac{b}{c+k}}+\sqrt[m]{\frac{c}{d+k}}+\sqrt[m]{\frac{d}{a+k}}\leq\begin{cases}
2\sqrt[m]{\frac{P_{2n-1}(\gamma)}{Q_{2n}(\gamma)}(\gamma+4)^{2n-1}},\quad S\geqslant 4k(2n-1)\\
4\sqrt[m]{\frac{S}{S+4k}},\quad S\leqslant 2k(2n-1)
\end{cases}$$ $$\sqrt[m]{\frac{a}{b+k}}+\sqrt[m]{\frac{b}{c+k}}+\sqrt[m]{\frac{c}{d+k}}+\sqrt[m]{\frac{d}{a+k}}\leq\begin{cases}
2\sqrt[m]{\frac{P_{2n-1}(\gamma)}{Q_{2n}(\gamma)}(\gamma+4)^{2n-1}},\quad S\geqslant 4k(2n-1)\\
4\sqrt[m]{\frac{S}{S+4k}},\quad S\leqslant 2k(2n-1)
\end{cases}$$](https://dxdy-02.korotkov.co.uk/f/1/1/3/11314df168c961842dc0adb09641c1a882.png)
где

- неотрицательный корень уравнения

____

![$$\sqrt[m]{\frac{a}{b+k}}+\sqrt[m]{\frac{b}{c+k}}+\sqrt[m]{\frac{c}{d+k}}+\sqrt[m]{\frac{d}{a+k}}\leq\begin{cases}
2\sqrt[m]{\frac{Q_{2n}(\gamma)}{P_{2n+1}(\gamma)}(\gamma+4)^{2n+1}},\quad S\geqslant 8kn\\
4\sqrt[m]{\frac{S}{S+4k}},\quad S\leqslant 4kn
\end{cases}$$ $$\sqrt[m]{\frac{a}{b+k}}+\sqrt[m]{\frac{b}{c+k}}+\sqrt[m]{\frac{c}{d+k}}+\sqrt[m]{\frac{d}{a+k}}\leq\begin{cases}
2\sqrt[m]{\frac{Q_{2n}(\gamma)}{P_{2n+1}(\gamma)}(\gamma+4)^{2n+1}},\quad S\geqslant 8kn\\
4\sqrt[m]{\frac{S}{S+4k}},\quad S\leqslant 4kn
\end{cases}$$](https://dxdy-01.korotkov.co.uk/f/8/2/6/826e81017c0ff9f112f1b75b0a38a24e82.png)
где

- неотрицательный корень уравнения

_______________________________________

тезисное рассуждение:
Рассмотрим функцию
![$F(x, s) =\sqrt[m]{\frac{x}{s-x+1}}+\sqrt[m]{\frac{s-x}{x+1}}$ $F(x, s) =\sqrt[m]{\frac{x}{s-x+1}}+\sqrt[m]{\frac{s-x}{x+1}}$](https://dxdy-04.korotkov.co.uk/f/f/d/4/fd42468c6bb217fa1eb577c59d82ec6382.png)
на



где


- неотрицательный корень уравнения


(не имеет положительных корней)
для

проверяем положительность коэффициентов многочлена

для

проверяем положительность коэффициентов многочлена

для

проверяем положительность коэффициентов многочленов

Поэтому уравнение

имеет три неотрицательных корня, при

и один неотрицательный корень при

Поэтому
![$$F_{\max}(s)=\begin{cases}
F(x_1,s)=F(x_2,s)=(\alpha+2)\sqrt[m]{\frac{P_{2n-1}(\alpha)}{P_{2n+1}(\alpha)}},\quad s\geqslant2n-1\\
F(\frac{s}{2},s)=2\sqrt[m]{\frac{s}{s+2}},\quad s\leqslant 2n-1
\end{cases}$$ $$F_{\max}(s)=\begin{cases}
F(x_1,s)=F(x_2,s)=(\alpha+2)\sqrt[m]{\frac{P_{2n-1}(\alpha)}{P_{2n+1}(\alpha)}},\quad s\geqslant2n-1\\
F(\frac{s}{2},s)=2\sqrt[m]{\frac{s}{s+2}},\quad s\leqslant 2n-1
\end{cases}$$](https://dxdy-01.korotkov.co.uk/f/0/7/d/07d0eeb28e4f21b48de58f0fd827782f82.png)
Т.о.
![$\sqrt[m]{\frac{x}{w+k}}+\sqrt[m]{\frac{w}{x+k}}=F(\frac{x}{k}, \frac{x+w}{k})\leqslant F_{\max}(\frac{x+w}{k})=\begin{cases}
(\alpha+2)\sqrt[m]{\frac{P_{2n-1}(\alpha)}{P_{2n+1}(\alpha)}},\quad x+w\geqslant k(2n-1)\\
2\sqrt[m]{\frac{x+w}{x+w+2k}},\quad x+w\leqslant k(2n-1)
\end{cases}$ $\sqrt[m]{\frac{x}{w+k}}+\sqrt[m]{\frac{w}{x+k}}=F(\frac{x}{k}, \frac{x+w}{k})\leqslant F_{\max}(\frac{x+w}{k})=\begin{cases}
(\alpha+2)\sqrt[m]{\frac{P_{2n-1}(\alpha)}{P_{2n+1}(\alpha)}},\quad x+w\geqslant k(2n-1)\\
2\sqrt[m]{\frac{x+w}{x+w+2k}},\quad x+w\leqslant k(2n-1)
\end{cases}$](https://dxdy-02.korotkov.co.uk/f/9/5/f/95f73f832bb6de75dd09af3469f53b1782.png)
где

- неотрицательный корень уравнения

____
Отметим для всех

:
Утверждение

функция
![$(\theta_t+2)\sqrt[m]{\frac{P_{2n-1}(\theta_t)}{P_{2n+1}(\theta_t)}}$ $(\theta_t+2)\sqrt[m]{\frac{P_{2n-1}(\theta_t)}{P_{2n+1}(\theta_t)}}$](https://dxdy-01.korotkov.co.uk/f/8/5/d/85da15b3a073dd82b85875b25421979382.png)
является вогнутой
Утверждение
![$T_2:\quad (\theta_t+2)\sqrt[m]{\frac{P_{2n-1}(\theta_t)}{P_{2n+1}(\theta_t)}}\geqslant F(\frac{t}{2},t)$ $T_2:\quad (\theta_t+2)\sqrt[m]{\frac{P_{2n-1}(\theta_t)}{P_{2n+1}(\theta_t)}}\geqslant F(\frac{t}{2},t)$](https://dxdy-03.korotkov.co.uk/f/6/e/7/6e7c7e1207d86e1a491a44d2e615440282.png)
тут

- наибольший (не обязательно неотрицательный) корень уравнения

____
Пусть

- это числа
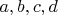
расположенные по возрастанию, тогда
![$\sqrt[m]{x}\leqslant\sqrt[m]{y}\leqslant\sqrt[m]{z}\leqslant\sqrt[m]{w}$ $\sqrt[m]{x}\leqslant\sqrt[m]{y}\leqslant\sqrt[m]{z}\leqslant\sqrt[m]{w}$](https://dxdy-04.korotkov.co.uk/f/7/c/e/7cec9fcd680ca564f1cf04c83359c69982.png)
![$\sqrt[m]{\frac{1}{w+k}}\leqslant\sqrt[m]{\frac{1}{z+k}}\leqslant\sqrt[2n]{\frac{1}{y+k}}\leqslant\sqrt[m]{\frac{1}{x+k}}$ $\sqrt[m]{\frac{1}{w+k}}\leqslant\sqrt[m]{\frac{1}{z+k}}\leqslant\sqrt[2n]{\frac{1}{y+k}}\leqslant\sqrt[m]{\frac{1}{x+k}}$](https://dxdy-01.korotkov.co.uk/f/8/c/8/8c8c7ad3770ee513e96d3d5f7225e54f82.png)
и по перестановочному неравенству
![$\sum\limits_{cyc}\sqrt[m]{\frac{a}{b+k}}\leqslant\left(\sqrt[m]{\frac{x}{w+k}}+\sqrt[m]{\frac{w}{x+k}}\right)+\left(\sqrt[2n]{\frac{y}{z+k}}+\sqrt[m]{\frac{z}{y+k}}\right)\leqslant$ $\sum\limits_{cyc}\sqrt[m]{\frac{a}{b+k}}\leqslant\left(\sqrt[m]{\frac{x}{w+k}}+\sqrt[m]{\frac{w}{x+k}}\right)+\left(\sqrt[2n]{\frac{y}{z+k}}+\sqrt[m]{\frac{z}{y+k}}\right)\leqslant$](https://dxdy-01.korotkov.co.uk/f/c/2/f/c2f747ee4ba2ddb683676d820bb68e8782.png)

Случай


![$= 2\sqrt[m]{\frac{x+w}{x+w+2k}}+2\sqrt[m]{\frac{y+z}{y+z+2k}}\stackrel{Jensen}\leqslant 4\sqrt[m]{\frac{\frac{x+y+z+w}{2}}{\frac{x+y+z+w}{2}+2k}}=4\sqrt[m]{\frac{S}{S+4k}}$ $= 2\sqrt[m]{\frac{x+w}{x+w+2k}}+2\sqrt[m]{\frac{y+z}{y+z+2k}}\stackrel{Jensen}\leqslant 4\sqrt[m]{\frac{\frac{x+y+z+w}{2}}{\frac{x+y+z+w}{2}+2k}}=4\sqrt[m]{\frac{S}{S+4k}}$](https://dxdy-01.korotkov.co.uk/f/c/2/d/c2d6449f4931445f4ffb50d74001ff7982.png)
Случай


![$(\theta_{(x+w)}+2)\sqrt[m]{\frac{P_{2n-1}(\theta_{(x+w)})}{P_{2n+1}(\theta_{(x+w)})}}+(\theta_{(y+z)}+2)\sqrt[m]{\frac{P_{2n-1}(\theta_{(y+z)})}{P_{2n+1}(\theta_{(y+z)})}}\stackrel{T_1\; and\; Jensen}\leqslant $ $(\theta_{(x+w)}+2)\sqrt[m]{\frac{P_{2n-1}(\theta_{(x+w)})}{P_{2n+1}(\theta_{(x+w)})}}+(\theta_{(y+z)}+2)\sqrt[m]{\frac{P_{2n-1}(\theta_{(y+z)})}{P_{2n+1}(\theta_{(y+z)})}}\stackrel{T_1\; and\; Jensen}\leqslant $](https://dxdy-04.korotkov.co.uk/f/3/9/b/39bb230f430ed41e67e891207348b0e082.png)
![$(\gamma+2)\sqrt[m]{\frac{P_{2n-1}(\gamma)}{P_{2n+1}(\gamma)}}$ $(\gamma+2)\sqrt[m]{\frac{P_{2n-1}(\gamma)}{P_{2n+1}(\gamma)}}$](https://dxdy-03.korotkov.co.uk/f/2/1/0/210970e07f80ed524954a5ed1f5590ad82.png)
где

- наибольший (не обязательно неотрицательный) корень уравнения


- неотрицательный корень уравнения

(условие

гарантирует такой корень. При остальных

эта оценка неравенства

сохраняется, но равенство уже не достигается).
_____________________
Оставшиеся случаи

рассматриваются, в общем аналогично, только уже для функции

поскольку у

проблемы с неотрицательностью одного из корней.