В книге М.М. Постникова ``Лекции по геометрии. Семестр 4. Дифференциальная геометрия'' (ссылка
здесь) сформулировано следующее утверждение:
Задача 13 (стр. 492)
Покажите, что 2-инстантоны с  и
и  параметризируются числом
параметризируются числом  и кватернионами
и кватернионами  и
и 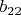 , удовлетворяющими неравенству
, удовлетворяющими неравенству  .
.В общем случае (стр. 491), 2-инстантон должен удовлетворять уравнению

, которое в данном случае тождественно выполняется, и системе уравнений

которая, по условию, должна иметь только тривиальное решение

и

для любого кватерниона

.
Вопрос: Как получается неравенство

? У меня, вместо него, выходит

.