Сначала докажем, что он ограничен (чтобы не предполагать, что он бесконечен).
Так это ведь ключевой момент -- что логарифм как минимум не превосходит степени. Дальше можно уже как угодно.
Ладно, вот самое простое доказательство, не требующее никакой изобретательности. Никто не сомневается, что при
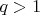
геометрическая прогрессия

растёт быстрее любой арифметической прогрессии; вопрос лишь, как это доказать формально. Ну так начнём с того, что она
не меньше какой-нибудь арифметической прогрессии. Такая прогрессия легко угадывается:

, где

.
Отсюда, между прочим, следует, что

(т.е. именно отсюда это следует автоматически; лобовое доказательство потребовало бы хоть какой-то, но казуистики). Соответственно, если

, то

.
Теперь из

следует

(где

, но это не важно). Откуда, между прочим, геометрическая прогрессия действительно оценивается снизу через любую арифметическую, но нам даже и это тоже не нужно.
Однако если оценка есть для любого
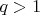
, то она есть и для какого-нибудь

(неважно, какого; скажем,

). Тогда

.
(Т.е. это утверждение относится к разряду тех, доказательство которых существенно упрощается после обобщения формулировки.)