Но у нас не было теоремы Дирихле, я посмотрел её доказательство - оно не простое.
Это в общем случае не простое, а в Вашем частном случае (для данного натурального

доказать, что существует бесконечно много простых чисел

) доказательство несложное (идея Евклида плюс свойства кругового многочлена

). В принципе, если его разобрать (а его и школьникам иногда рассказывают), то, может быть, и польза будет.
Но лучше, конечно, что-нибудь без Дирихле придумать.
Upd. Да, без Дирихле вполне можно обойтись. Достаточно того факта, что группы
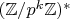
--- циклические (

--- нечетное простое,

--- натуральное). Это довольно известный факт (теорема Гаусса).