В связи с коронавирусными делами встали такие вопросы.
1. Есть процесс Бернулли с неизвестным

, и есть выборка. Размер выборки

, количество успехов

Надо найти доверительный интервал для оценки

- вероятности успеха.
Почитал\погуглил, в том числе соответствующую тему на форуме... В частности, открыл "букварь" В.Е. ГМУРМАН. Руководство к решению задач по теории вероятностей и математической статистике.
Там указано две формулы:
Более точная:

Приближенная, для больших

:

Где:

,

- значение аргумента функции Лапласа, при котором

(

— заданная надежность).
Вроде бы, первая формула сводится ко второй при больших

вне зависимости от

. Но меня гложут смутные сомнения о применимости этих формул для малых

.
2. Пусть некая величина

рассчитывается так

, где

- оценки вероятностей для независимых процессов Бернулли.
Будет ли верно считать её доверительный интервал (например, для

) так:
а) посчитаем доверительные интервалы для
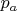
и

для

б) после этого посчитаем границы доверительного интервала для

так:
нижняя граница граница: значение

для максимального
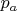
и минимального

верхняя граница: значение

для минимального
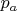
и максимального
