Consider the triangle (angles

)
![$$
\begin{tikzpicture}
\coordinate [left] (A) at (0, 0)
\coordinate [above] (B) at (2, 2)
\coordinate [right] (C) at (3, 0)
\coordinate [left] (D) at (0.667, 0.667)
\draw (A) node[left] {$A$} -- (B) node[above] {$B$} -- (C) node[right] {$C$} -- cycle;
\path (A) -- (D) node [pos=0.5, left] {$p$}
\path (D) -- (B) node [pos=0.5, left] {$q$}
\node[left] at (D) {$D$}
\draw (C)--(D) node [pos=0.5, above] {$d$}
\end{tikzpicture}
$$ $$
\begin{tikzpicture}
\coordinate [left] (A) at (0, 0)
\coordinate [above] (B) at (2, 2)
\coordinate [right] (C) at (3, 0)
\coordinate [left] (D) at (0.667, 0.667)
\draw (A) node[left] {$A$} -- (B) node[above] {$B$} -- (C) node[right] {$C$} -- cycle;
\path (A) -- (D) node [pos=0.5, left] {$p$}
\path (D) -- (B) node [pos=0.5, left] {$q$}
\node[left] at (D) {$D$}
\draw (C)--(D) node [pos=0.5, above] {$d$}
\end{tikzpicture}
$$](https://dxdy-03.korotkov.co.uk/f/e/d/4/ed4439902771fea25281b0248123d1c482.png)
Let

be the angle
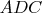
. Using the sine theorem

and multiplying both
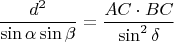
On the other hand, let
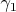
be the angle

so
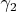
is defined using
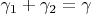
. We use the same trick again
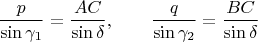
now multiplying both and inserting earlier equations yields
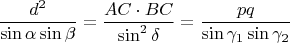
So if
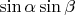
exceeds the maximal value of
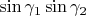
, we are in trouble :) And what
is that maximal value is a completely separate question.
We can make an observation. The value of

is between
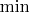
and
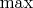
of the pair
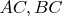
. So, if
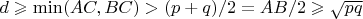
, there are no

points such that
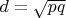
. Consider
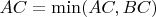
for certainty. We have
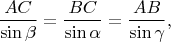
and if
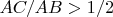
, we have
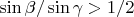
. Generally speaking,
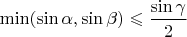
is an additional constraint. Is it automatically fulfilled? We have
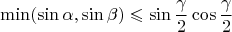
and
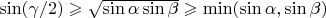
,
but here we have a

in the right side, so it occurs to be a stronger constraint than presented!