Задача, похоже, не вызвала особого интереса. А между тем, вопрос-то весьма любопытный. Начать с того, что единственность при минимальных естественных условиях известна очень давно (Титчмарш. Введение в теорию интегралов Фурье.). А вот с разрешимостью проблемы.
Один из типичных способов решения таких уравнений --- с помощью дифференцирования получить уравнение второго рода. Этот прием сработает, если функция

гладкая и найдется ненулевая производная

. А если гладкость закончится раньше, или все производные нулевые? Кстати, данный подход показывает, что гладкость решения может быть существенно хуже гладкости правой части
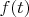
. Например, для

имеем

. Кроме гладкости, правая часть еще и должна иметь нуль ''подходящего'' порядка при
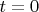
, но это сейчас не важно. Значит решения нашего уравнения способны со временем терять гладкость. Действительно, при

значения

можно определять из уравнения

Но в правой части появляется функция
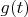
, которая может быть менее гладкая, чем
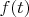
. Из этих соображений уже легко строится искомый пример. Положим

Для гладкой
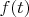
, такой, что

имеем

Из этой формулы видно, что гладкость решения уменьшается при переходе через

.
А что с преобразованием Лапласа?
Если совершенно формально как-то продолжить все функции на полуось

и применить преобразование Лапласа, то получим

Отсюда видна главная проблема. Знаменатель может быть малым или даже нулевым. У нас есть определенный произвол в выборе продолжений функций

, но совершенно непонятно как им ''грамотно'' распорядиться. Как убрать возможные особенности

в некоторой полуплоскости

? Кроме этого, надо еще и обеспечить сходимость интеграла в обратном преобразовании

Оказывается, все не так уж и сложно. Не надо искать какие-то замечательные продолжения функций. Надо просто сдвинуть контур интегрирования в ту область, где

ведет себя ''хорошо''. Просто так отодвинуть прямую не получается. Нужен ''кривой'' контур. Отметим, что этому мешает экспонента

. Под интегралом для экспоненты мы можем позволить себе не более чем степенной рост по
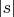
. Этот рост можно скомпенсировать быстрым (степенным) убыванием

. Такое убывание дает гладкость
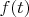
и нужное обращение в 0 при
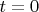
. Таким образом, на контуре мы должны иметь что-то типа

Правее этого контура требуется поведение от

. Легко видеть, что все это как раз и обеспечивается условием

Таким образом мы получили формальное представление для решения при

. Легко убедиться, что это действительно решение. Значит условие (2) достаточно для разрешимости уравнения (1), при условии, что правая часть достаточно гладкая и как-то-там обращается в 0 при
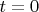
. Но условие (2) и необходимо для разрешимости уравнения (1). Для этого достаточно рассмотреть

. Пусть

таково, что решение существует при


Все функции продолжаем нулем при

.
Умножим это уравнение на

и проинтегрируем по

. После нехитрых преобразований легко получаем

Отсюда следует условие (2).
К сожалению, с практической точки зрения от этих результатов мало толку. Хотя и удается строить разные экзотические примеры. Например, такой пример несуществования локального решения.
Пусть

имеет бесконечное количество нулей на вещественной полупрямой

. Тогда уравнение

не разрешимо ни на каком интервале

для любой нетривиальной функции

. Ни гладкость, ни обращение в нуль, ничего не помогает. Для доказательства достаточно рассмотреть частичное преобразование Лапласа (как и при доказательстве необходимости) с конкретными значениями

--- вещественными нулями

, и устремить

. Левая и правая часть равенства будут иметь разную скорость стремления к 0.
Еще один экзотический пример. Можно указать негладкое ядро

, у которого даже нет конечной вариации в окрестности
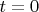
, а разрешимость уравнения есть.
Это просто ступенчатая функция со значениями 0 и 1, которая ''нужным'' образом осциллирует в окрестности
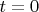
. Для нее можно проверить справедливость условия (2).