Цитата:
Let

be a universe of objects and let
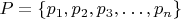
be a set of properties that the objects may or may not have. For any

let
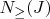
equal the number of objects in

that have the properties in

and possibly others, and
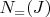
-- the number of objects in

that have the properties in

and no others. Show the number of objects in

with none of the properties is
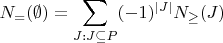
.
Proof(?) with holes:
Suppose
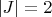
. Then some of the
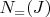
s are
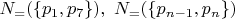
etc. There are

such
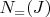
s. Generally, if
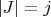
, then there are
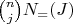
objects all of whose properties are in

meaning
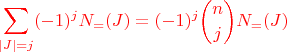
. Summing both sides of the expression in

above, we have
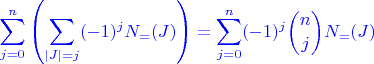
Since removing objects with
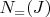
properties also removes objects with
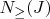
properties(think of overlapping sets

where

can also be in

), we can replace
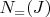
s in the expression

above with
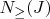
s as follows:
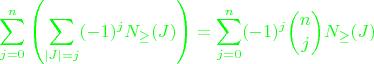
Note that the number of objects in

with none of the properties is
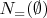
meaning the number of times
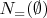
includes each object in

is

when the object has none of the properties and

when the object has at least one property. If we can say the same thing about the expression
above, then we can use it instead of
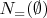
.
Now assume an object in

contains none of the properties in

. Then
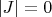
meaning
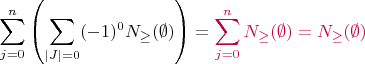
. [Here we want to be able to say "the expression
above counts an object with no properties in

only once". Exactly how, though?].
Suppose an object in

contains

properties in

where
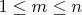
. Then
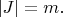
Now
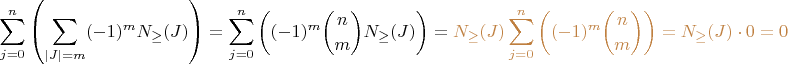
. Thus the expression
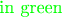
above doesn't even count an object with properties in

.
----------------------
У данного док-ва по меньшей мере три недостатка. Первый выделен фиолетовым цветом. С одной стороны кажется, что
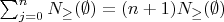
, но с другой -- у выражения нет индексов. Другой вопрос задан непосредственно за фиолетовым выражением. Третьи недостаток выделен коричневым цветом. Здесь была попытка использовать
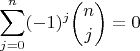
, но индексы в коричневой части не согласуются. Как это можно исправить?