(Оффтоп)
Если
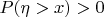
, то просто по определению условной вероятности, с учетом того что

и

- это просто одно и то же событие.
Если
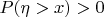
, то ваши рассуждения не проходят - нельзя брать условную вероятность относительно условия нулевой вероятности.
Во втором случае вы, видимо, имели в виду

Если
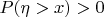
, то просто по определению условной вероятности, с учетом того что

и

- это просто одно и то же событие.
Здесь меня смущает, что все-таки

, а не

. То есть вполне может быть, что найдутся какие-то исходы, когда

, просто вероятность их нуль. В таком случае, строго говоря (насколько я понимаю),

Поэтому, когда я использую условную вероятность, вроде бы все встает на свои места.
Если

, то ваши рассуждения не проходят - нельзя брать условную вероятность относительно условия нулевой вероятности.
Ааа, ну да. В таком случае

, и автоматически

.
Так вам вопрос неясен, или что делать неясно?
Вопрос в целом ясен, кроме как вот это
при условии, что

и

определены на одном вероятностном пространстве
Я не мастак в тервере, и не очень пока могу понять, к чему это вообще...
Если второе - то обратите внимание, что

зависит только от распределения

и

и не зависит от их совместного распределения, а

- зависит от совместного распределения.
Ух, хорошо, спасибо, попробую покумекать над этим.