Доброго времени суток, уважаемые форумчане!
Пусть дана обратная задача нахождения функции

по имеющимся значениям



![$$
u_1(x,0)=0, \ \ x\in[0,x_0];\qquad u_2(x,0)=0,\ \ x\in \left( \right. x_0,1 \left. \right],
$$ $$
u_1(x,0)=0, \ \ x\in[0,x_0];\qquad u_2(x,0)=0,\ \ x\in \left( \right. x_0,1 \left. \right],
$$](https://dxdy-04.korotkov.co.uk/f/f/d/e/fde2d37ca0f0cbba354445ef1bc5710a82.png)





И также имеется алгоритм численного решения методом проекционной регуляризации с исходными данными
 1.
1. Применяем к

преобразование Фурье, находим

.
2. Нахождение

методом проекционной регуляризации

Значение параметра регуляризации

получим из принципа невязки

Обозначим полученное значение параметра регуляризации через

.
3. Применяя обратное преобразование Фурье

, получаем приближенное решение

![$$
h_\delta(t)=
\begin{cases}
\operatorname{Re}[F^{-1}[\hat{h}_\delta(\tau)]], & t \in [0,T],\\
0, & t \notin [0,T].
\end{cases}
$$ $$
h_\delta(t)=
\begin{cases}
\operatorname{Re}[F^{-1}[\hat{h}_\delta(\tau)]], & t \in [0,T],\\
0, & t \notin [0,T].
\end{cases}
$$](https://dxdy-03.korotkov.co.uk/f/e/3/2/e32d39687b026f3648ce479482aae66c82.png)
В качестве модельного примера была выбрана функция
![$
h_0(t)=
t\sin(\pi t), & t \in [0,1].
$ $
h_0(t)=
t\sin(\pi t), & t \in [0,1].
$](https://dxdy-02.korotkov.co.uk/f/1/8/3/183ee9afdafa74ecf78652b0cb1b2a3982.png)
Попробовал реализовать, вот что получилось (не судите строго)
public alglib.complex OperatorT(double r, double a1, double a2, double x0, double tau)
{
double arg2 = (1 - x0) * Math.Sqrt(tau) / a2 / Math.Sqrt(2);
double arg1 = arg2 + x0 * Math.Sqrt(tau) / a1 / Math.Sqrt(2);
alglib.complex T = new alglib.complex();
if (tau == 0) {
T.x = (x0 * a2 + a1 + x0 * a1) / (a1 - x0 * a1); // находится с помощью предела
T.y = (x0 * a2 + a1 + x0 * a1) / (a1 - x0 * a1);
}
else if (tau > r) { T.x = 0; T.y = 0; } // применение параметра регуляризации
else
{
T.x = (Math.Sinh(arg1) * Math.Cos(arg1) * Math.Sinh(arg2) * Math.Cos(arg2)
+ Math.Cosh(arg1) * Math.Sin(arg1) * Math.Cosh(arg2) * Math.Sin(arg2))
/ (Math.Sinh(arg2) * Math.Cos(arg2) * Math.Sinh(arg2) * Math.Cos(arg2)
+ Math.Cosh(arg2) * Math.Sin(arg2) * Math.Cosh(arg2) * Math.Sin(arg2));
T.y = (Math.Cosh(arg1) * Math.Sin(arg1) * Math.Sinh(arg2) * Math.Cos(arg2)
- Math.Sinh(arg1) * Math.Cos(arg1) * Math.Cosh(arg2) * Math.Sin(arg2))
/ (Math.Sinh(arg2) * Math.Cos(arg2) * Math.Sinh(arg2) * Math.Cos(arg2)
+ Math.Cosh(arg2) * Math.Sin(arg2) * Math.Cosh(arg2) * Math.Sin(arg2));
}
return T;
}
private void ButtonS_Click(object sender, RoutedEventArgs e)
{
int n = 512; // число узлов разбиения временного отрезка
alglib.xparams _params = new alglib.xparams(9);
alglib.complex [] a1 = new alglib.complex[n];
alglib.complex [] a2 = new alglib.complex[n];
alglib.complex[] a3 = new alglib.complex[n];
double [] r1 = new double[n];
double [] r2 = new double[n];
double[] r3 = new double[n];
double t = 1; // длина временного отрезка
double h = (double)t / (n - 1); //шаг разбиения
double[] xS = new double[n];
double[] Fs = new double[n];
double delta = 0.01; // уровень погрешности в начальных данных
Random r = new Random();
for (int i = 0; i <= n - 1; i++)
{
xS[i] = i * h;
r1[i] = xS[i] * Math.Sin(Math.PI * xS[i]); // функция из модельного примера
}
double x0 = 0.5, aa1 = 1, aa2 = 1; // ввод начальных данных
Par(r1, x0, ref r2); // нахождение r2 из решения прямой задачи в точке x0
// r2 - значения функции f(t), используемой в качестве начальных данных для обратной задачи
for (int i = 0; i <= n - 1; i++)
{ // внесение шума в начальные данные
double temp = -1 + 2 * r.NextDouble();
double dt = delta * temp / Math.Sqrt(t);
a1[i].x = r2[i] + dt;
a1[i].y = 0;
}
alglib.fft.fftc1d(ref a1, n, _params); // прямое преобразование Фурье
double td = 200; // длина отрезка по тау
double th = (double)td / (n - 1); // шаг разбиения
double R = 6; // параметр регуляризации
for (int i = 0; i <= n - 1; i++)
{ // оператор в методе проекионной регуляризации
alglib.complex T2 = new alglib.complex();
T2 = OperatorT(R, aa1, aa2, x0, i * th);
a2[i].x = (a1[i].x * T2.x - a1[i].y * T2.y);
a2[i].y = (a1[i].x * T2.y + a1[i].y * T2.x);
}
alglib.fft.fftc1dinv(ref a2, n, _params); // обратное преобразование Фурье
for (int i = 0; i <= n - 1; i++)
{
r3[i] = a2[i].x; // выделение Re
}
// отображение графиков
var X = xS.AsXDataSource();
var Y = r3.AsYDataSource();
var FS = r1.AsYDataSource();
CompositeDataSource compositeDataSource = X.Join(Y);
CompositeDataSource compositeDataSourceF = X.Join(FS);
plotter.AddLineGraph(compositeDataSource, Colors.Green, 2, "приближенное");
plotter.AddLineGraph(compositeDataSourceF, Colors.Red, 2, "точное");
}
Вот что получается
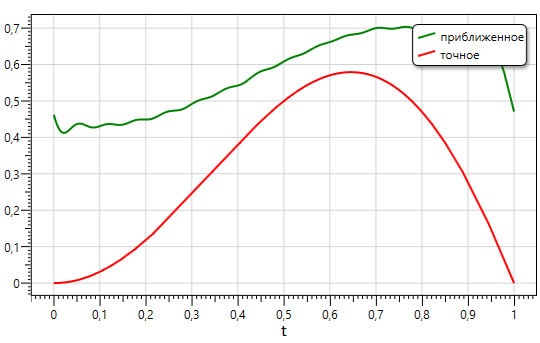
Меняя параметр регуляризации R, а также длину

ничего лучше получить не удается. Само собой такое решение никуда не годится. Возможно я что-то делаю принципиально неправильно. Помогите, пожалуйста, разобраться.
Может есть примеры реализации подобной задачи, например, на MATLAB?



