Известна формула:

Из этой формулы вытекает, что среднее значение функции
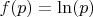
равно:
![$$E[f,n]=1+O(1/\ln(n)),$$ $$E[f,n]=1+O(1/\ln(n)),$$](https://dxdy-04.korotkov.co.uk/f/7/d/0/7d093a284936a116a100451ee66c892082.png)
поэтому
![$$\lim_{n \to \infty} E[f,n]=1,$$ $$\lim_{n \to \infty} E[f,n]=1,$$](https://dxdy-04.korotkov.co.uk/f/3/2/c/32ca238fb62b66f147ff011eba5771d682.png)
т.е среднее значение

на интервале

равно 1.
При этом, только при одном значении

. При всех остальных значениях:

и принимает сколь угодно большие значения. Где ошибка?