Вот это точно неверно - левая часть зависит от

, правая нет. И что за

в пределах интегрирования?
Плюс вы первообразную ищете, или сразу определенный интеграл? В первом случае вообще не должно быть пределов интегрирования, во втором - первое слагаемое должно быть не

, а

просто не знал как писать пределы в первообразной, теперь вижу:

, где:

- регулярная точка.
Stensen
А зачем Вам вообще по частям? Там же предлагают сравнить логарифм с какой-то подходящей степенью.
Если правильно понимаю, т.к.
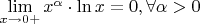
, тогда:
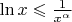
для

, тогда:

, для

, но из написанного, если правильно понял, это верно для :
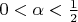
. Где я ошибаюсь?



