Частица на шероховатой плоскости

[pogulyat_vyshel]

Плоскость наклонена под углом $\alpha$ к горизонтали.
На плоскость кладут массивную частицу и придают ей начальную скорость в горизонтальном направлении. Коэффициент сухого трения равен $\gamma.$
Найти необходимые и достаточные условия на параметры $\alpha,\gamma$ при которых траектория частицы имеет асимптоту.

[rascas]

$\tg\alpha \geqslant \gamma > 0$

[pogulyat_vyshel]

Нет

[Ignatovich]

(Оффтоп)

$\gamma\leqslant\tg\alpha \leqslant 2\gamma$

[pogulyat_vyshel]

Да, верно, только одно из неравенств должно быть строгим как я помню

[rascas]

Расположим ось Oy в наклонной плоскости, перпендикулярно линии пересечения наклонной плоскости и горизонтальной плоскости, направлением вниз.
Соответственно ось Ox в наклонной плоскости, параллельно линии пересечения наклонной плоскости и горизонтальной плоскости.
Т.о. материальная точка движется в плоскости xOy.

Будем рассматривать граничный случай: $\tg \alpha = \gamma$, и докажем, что траектория движения м.т. в этом случае бесконечная линия и имеющая асимптоту параллельную оси Oy.

Рассматриваем время, когда траектория движения м.т. уже стабилизировалась в движении вдоль асимптоты.
$t_0=0$,
$v_y$ - составляющая скорости вдоль Oy,
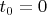
$v_x$ - составляющая скорости вдоль Ox, $v_x \ll v_y$
$\beta$ - угол между скоростью и Oy. $\tg \beta = \frac {v_x} {v_y} \approx \beta \approx \sin \beta $
$m$ - масса материальной точки (масса частицы)

$F$ - проекция силы тяжести на наклонную плоскость, направлена вдоль Oy.
$F_t$ - сила трения, направлена встречно к скорости движения, а по величине $F_t = F$ (случай $\tg \alpha = \gamma$).


Рассмотрим приращение скоростей в $t_1 = dt$
$d v_x = -\frac {F_t} {m} \beta dt$
$d \beta = \frac {d v_x} {v_y} = -\frac {F_t } {m v_y} \beta dt$

решаем ДУ: $\frac {d \beta} {\beta} = -\frac {F_t } {m v_y} dt$

$\beta = \beta_0 e^{-\frac {F_t } {m v_y} t}$

Видно, что со временем траектория асимптотически становится параллельна оси Oy ($\beta \to 0$).

В случае $\tg \alpha > \gamma$ м.т. будет двигаться с ускорением вдоль оси Oy тем более будет асимптота.

В случае $\tg \alpha < \gamma$ м.т. остановится, длина траектории ограничена, нет асимптоты.

Т.о. доказана правильность моего ответа:

rascas в сообщении #1479849 писал(а):

$\tg\alpha \geqslant \gamma > 0$

[amon]

rascas в сообщении #1479896 писал(а):

В случае $\tg \alpha > \gamma$ м.т. будет двигаться с ускорением вдоль оси Oy тем более будет асимптота.

Это утверждение в общем случае неверно.

[rascas]

amon в сообщении #1479898 писал(а):

rascas в сообщении #1479896 писал(а):

В случае $\tg \alpha > \gamma$ м.т. будет двигаться с ускорением вдоль оси Oy тем более будет асимптота.

Это утверждение в общем случае неверно.

Что качественно поменяется в моём решении, что приведёт к отсутствию асимптоты?

[amon]

rascas в сообщении #1479899 писал(а):

Что качественно поменяется в моём решении, что приведёт к отсутствию асимптоты?

Пусть $\gamma=0.$ В этом случае асимптоты нет (парабола не имеет асимптоты), а все Ваше рассуждение начиная с "Рассматриваем время, когда траектория движения м.т. уже стабилизировалась в движении вдоль асимптоты..." гаммы не содержит и, стало быть, остается в силе и для параболы.

[rascas]

amon в сообщении #1479903 писал(а):

Пусть $\gamma=0.$

Мой ответ был:

rascas в сообщении #1479849 писал(а):

$\tg\alpha \geqslant \gamma > 0$

Случай $\gamma=0$ разумеется не рассматриваем.
Так всё же , что с решением не так при $\tg\alpha > \gamma$ (при строго положительном $\gamma$) ?

[amon]

rascas в сообщении #1479904 писал(а):

Так всё же , что с решением не так

Из $\lim\limits_{t\to\infty}\beta=0$ не следует, что у траектории есть асимптота, параллельная оси $Y$. Контрпример - свободное падение с горизонтальной начальной скоростью: $V_x=v,\,V_y=gt.$