плиз, поподробнее о параметре
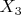
, конкретно, может ли он принимать отрицательные значения?
Добавлено спустя 2 часа 2 минуты 33 секунды:
вот что получилось(выкладываю листинг):
6 6 - число параметров, число функций
0.00 1.00 2.00 - ax, начальное приближение для 1-го параметра, bx
0.00 500.00 2000 - ax, начальное приближение для 2-го параметра, bx
0.00 20.00 2000 - ax, начальное приближение для 3-го параметра, bx
-1.57 0.00 1.57 - ax, начальное приближение для 4-го параметра, bx
-1.57 0.00 1.57 - ax, начальное приближение для 5-го параметра, bx
0.00 0.18 1.00 - ax, начальное приближение для 6-го параметра, bx
значение лок. минимума f0= 0.6228E+10
точка лок.минимума : 0.8610E+01 0.5670E+03 0.5629E+03 0.1580E+01 -0.1023E+01 0.3715E+01
n_count_fun = 1874
новая точка старта ( F(x0) <= f0 ) : 0.3149E+00 0.1889E+03 0.1316E+03 -0.4344E+00 -0.7932E+00 0.7707E+00
CALL search_negative_value_fun :
f0 = 0.6228E+10
F(x_new) = 0.1466E+10
Число обращений к ф-ии = 3489
max_iter = 1614
ierr = 0
значение лок. минимума f0= 0.5842E-03
точка лок.минимума : 0.5000E+00 0.1844E+03 0.1166E+03 -0.1090E+01 -0.5664E+00 0.8252E+00
n_count_fun = 4389
ierr = -1 ( мои коммент: диагностирует, что более глубокого минимума нет)
Результаты :
значение минимума f0= 0.5842E-03 ( мои коммент: это сумма квадратов невязки - то, что минимизировалось)
точка минимума : 0.5000E+00 0.1844E+03 0.1166E+03 -0.1090E+01 -0.5664E+00 0.8252E+00
( мои коммент: -0.1090E+01 -0.5664E+00 - углы в радианах )
1 -1.1793233E-02
2 -1.2702820E-03
3 -3.9257156E-03
4 4.2474824E-03
5 -6.2746224E-03
6 -7.0310775E-03
( мои коммент: первый стлобец - номер уравнения, второй - невязка).
( конец листинга)
критерий точности по параметрам задавался 0.0001,
ну, если задать типа 1.е-10, наверно невязки будут нулевые.