Типа бином. распределение, но с разными вер-ми успеха

[melnikoff]

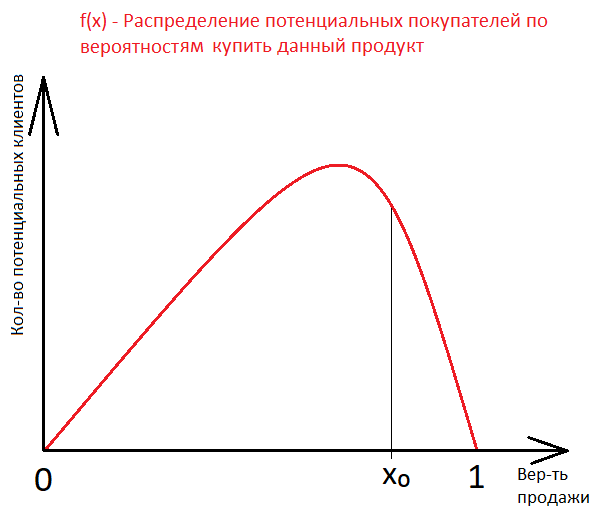
Имеется фактическое распределение (гистограмма) большого числа потенциальных покупателей ($N$) по вероятностям покупки данного товара.
Допустим, мы предлагаем товар только тем покупателям, для которых соответствующая вероятность продажи $p$ лежит в границах $x_0 \leq p \leq 1$ (см. рисунок).
Нужно найти:
1) Мат. ожидание кол-ва продаж;
2) Наиболее вероятное значение кол-ва продаж;
3) Цель-максимум: Построить случ. величину $\xi$ – кол-во продаж.

Вообще, постановка задачи похожа на биномиальное распределение (распределение по вероятностям количеств успехов), вот только тут вероятности успеха для разных попыток разные. С этим трудности.
Для начала вычислим количество предложений (попыток): $M=\int\limits_{x_0}^{1}f(x)$
Далее, чтобы найти мат. ожидание кол-ва продаж есть идея разбить интервал $x_0 \leq p \leq 1$ на $k$ равных интервалов и на каждом из них рассмотреть кол-во продаж как биномиальное распределение (с последующим устремлением $k$ к бесконечности): $p_k=\frac{x_k + x_{k-1}}{2}$ – вероятность успеха на k-m интервале, а $f_k=\frac{\int\limits_{x_{k-1}}^{x_k}f(x)}{x_k - x_{k-1}}$ - среднее значение $f(x)$ на k-m интервале. Мат. ожидание на k-м интервале равно $M_k=p_kf_k$.

Тогда мат. ожидание на интервале $x_0 \leq p \leq 1$ будет равно сумме мат. ожиданий на составляющих интервалах (предположение):
$M[\xi] = \sum\limits_{1}^{k}p_kf_k$.
Насколько правилен этот подход?
Вопрос что делать с пунктами 2 и 3 остается открытым. Прошу помощи.

[Lia]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

melnikoff
Одинокие буковки - это тоже формулы, оформляйте их соответственно.
- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы);
- отсутствуют собственные содержательные попытки решения задач(и).

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

[Lia]

Тема перемещена из форума «Карантин» в форум «Помогите решить / разобраться (М)»

[mihaild]

melnikoff в сообщении #1476808 писал(а):

Тогда мат. ожидание на интервале $x_0 \leq p \leq 1$ будет равно сумме мат. ожиданий на составляющих интервалах

Представьте себе, что $f$ вообще постоянна. Тогда $f_k$ все одинаковые. И с увеличением числа точек в разбиении сумма неограниченно растет.
Вам точно нужен непрерывный случай? Если покупателей конечное число, то количество покупок распределено по биномиальному распределению Пуассона.