Тут интереснее поставить вопрос, при каких еще

(например, вида

, где

- целые) и соответственно величинах шага наблюдается подобный эффект?
В матричной форме эффект выражается в том, что при некоторых

и

матрица

возведённая в степень

, внезапно пропорциональна единичной матрице.
Пусть

, тогда собственные значения

равны

. Их аргумент равен

и после умножения на

должен быть кратен

. Отсюда

Значение

получается при
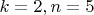
.
Значение

получается при

.
При каких

и

формула даёт числа вида

— этого я не знаю. Вопрос сводится к тому, когда такой вид имеет

или
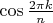
.