Пусть

есть самосопряженный оператор, действующий в гильбертовом пространстве

. Пусть для простоты

компактен. Предположим, что для некоторой константы

выполнено

. Тогда для
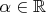
можно определить дробную степень оператора

при любом

и пространства

со скалярным произведением

. Пространство

как множество от выбора

не зависит, а соответствующие скалярные произведения эквиваленты.
Рассмотрим

-полугруппу

(в

), порожденную оператором

.
Рассмотрим решение неоднородной задачи

с

на промежутке
![$[0,T]$ $[0,T]$](https://dxdy-03.korotkov.co.uk/f/a/a/b/aab0f08201b211261f795050337fa8df82.png)
для

. Оно дается формулой

Из общей теории

-полугрупп имеем
![$v(\cdot) \in C([0,T];\mathbb{H})$ $v(\cdot) \in C([0,T];\mathbb{H})$](https://dxdy-04.korotkov.co.uk/f/f/5/3/f5342dbb305dec8f25f8d8c4607c9e4782.png)
. Пусть

. Меня интересует, что можно сказать про принадлежность решения

более хорошим пространствам. Например, можно ли, утверждать, что
1)
![$v(\cdot) \in C([0,T];\mathbb{H}_{\alpha})$ $v(\cdot) \in C([0,T];\mathbb{H}_{\alpha})$](https://dxdy-03.korotkov.co.uk/f/a/9/a/a9a0f82caab45ba122043662f116fab082.png)
, или 2)

или, те же вопросы, если потребовать дополнительно, что

(и все том же

).
Насколько я понимаю, Теорема 1.2 главы 3 из Lions J. L. Optimal control of systems governed by partial differential equations, 1971 дает ответ при

(иначе оператор

не продолжить до оператора

с коэрцитивной относительно

формой). А именно получаем, что

. В частности, при

будет

. Можно ли усилить это для

, дополнительно потребовав

, или

все испортит?