Евгений Машеров, я не хотел расписывать подробно и видимо потерял часть смысла.
Пусть есть совокупность наблюдение

, где:
-
![$i \in [1 : N]$ $i \in [1 : N]$](https://dxdy-03.korotkov.co.uk/f/2/f/b/2fb6923c7c651f7bb2e8fb58745072a182.png)
-

— вектор состояния в момент времени

;
-

— наблюденное значение в момент времени

;
-

— матрица (полного ранга) наблюдений в момент времени

;
-

— шумы наблюдений, многомерные нормальные попарно некоррелируемые случайные величины с единичной дисперсией.
Предполагается, что

, однако по в каждом конкретном эксперименте

, и мы не можем вычислить

, применив МНК к каждому наблюдению отдельно. Зато мы можем:
1. Предположить, что

это значение некоторого стохастического процесса

с нулевым матожиданием и известной ковариационной функцией

в момент времени

. В этом случае оценкой будет

где

;

;

— блочно-диагональная матрица, на

-том месте которой стоит

;

— блочная матрица, на

-том месте которой стоит матрица

.
2. Предположить, что все вектора

одинаковы. Тогда:

Введя блочный вектор

, в

-том блоке которого стоит единичная матрица размера

, мы можем записать эту оценку в терминах предыдущей:

Вопрос в следующем: очевидно, если брать некоторые типы случайных процессов (которые имеют огромную ковариацию первого состояния

и почти нулевую ковариацию разностей

), то оценка
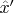
должна пости свопасть сло второй оценкой:

для любых

. Но доказать это у меня не получилось из-за того, что формула
Вудбюрри и формула обращения возмущенной матрицы

не работают: им мешает необратимость матрицы

.
Возможно, кто-то догадывается, как это проще доказать.