Я уже спрашивал, но вы ничего не ответили
Видимо пропустил. Тут довольно активное обсуждение было:)
Вы предлагаете верить вам на слово ?
Я предлагаю предполагать добрые намерения, и считать, что неотвеченный вопрос остался таковым по причинам, отличным от желания что-то подтасовать.
Процедура очень простая: берем все дроби вида

где

и

, умножаем каждую дробь на

и арифметически округляем. Дальше считаем, сколько раз получилось каждое значение от

до

. Получаем вот такой график
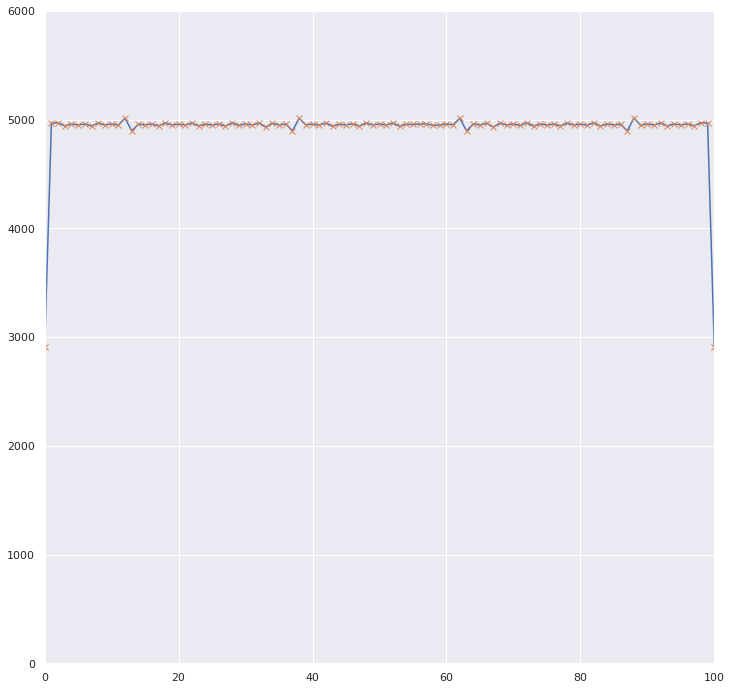
Пары (значение, доля), отсортированные по доле:
(Оффтоп)
(12, 0.010101701879943841),
(88, 0.010101701879943841),
(38, 0.010097673284976766),
(62, 0.010097673284976766),
(2, 0.01001710138563524),
(28, 0.01001710138563524),
(72, 0.01001710138563524),
(98, 0.01001710138563524),
(8, 0.010011058493184625),
(18, 0.010011058493184625),
(32, 0.010011058493184625),
(42, 0.010011058493184625),
(68, 0.010011058493184625),
(82, 0.010011058493184625),
(92, 0.010011058493184625),
(22, 0.010009044195701085),
(48, 0.010009044195701085),
(52, 0.010009044195701085),
(78, 0.010009044195701085),
(1, 0.01000501560073401),
(34, 0.01000501560073401),
(66, 0.01000501560073401),
(99, 0.01000501560073401),
(46, 0.009996958410799858),
(57, 0.009996958410799858),
(4, 0.009992929815832781),
(6, 0.009992929815832781),
(10, 0.009992929815832781),
(16, 0.009992929815832781),
(26, 0.009992929815832781),
(30, 0.009992929815832781),
(36, 0.009992929815832781),
(50, 0.009992929815832781),
(64, 0.009992929815832781),
(70, 0.009992929815832781),
(74, 0.009992929815832781),
(84, 0.009992929815832781),
(90, 0.009992929815832781),
(94, 0.009992929815832781),
(96, 0.009992929815832781),
(14, 0.009988901220865706),
(20, 0.009988901220865706),
(24, 0.009988901220865706),
(40, 0.009988901220865706),
(44, 0.009988901220865706),
(56, 0.009988901220865706),
(60, 0.009988901220865706),
(76, 0.009988901220865706),
(80, 0.009988901220865706),
(86, 0.009988901220865706),
(54, 0.009986886923382166),
(55, 0.009982858328415091),
(39, 0.009976815435964476),
(61, 0.009976815435964476),
(5, 0.0099727868409974),
(9, 0.0099727868409974),
(15, 0.0099727868409974),
(19, 0.0099727868409974),
(21, 0.0099727868409974),
(25, 0.0099727868409974),
(31, 0.0099727868409974),
(35, 0.0099727868409974),
(41, 0.0099727868409974),
(45, 0.0099727868409974),
(49, 0.0099727868409974),
(51, 0.0099727868409974),
(59, 0.0099727868409974),
(65, 0.0099727868409974),
(69, 0.0099727868409974),
(75, 0.0099727868409974),
(79, 0.0099727868409974),
(81, 0.0099727868409974),
(85, 0.0099727868409974),
(91, 0.0099727868409974),
(95, 0.0099727868409974),
(11, 0.009968758246030324),
(89, 0.009968758246030324),
(29, 0.009964729651063247),
(58, 0.009964729651063247),
(71, 0.009964729651063247),
(3, 0.009956672461129095),
(23, 0.009956672461129095),
(77, 0.009956672461129095),
(97, 0.009956672461129095),
(7, 0.009954658163645555),
(17, 0.009954658163645555),
(83, 0.009954658163645555),
(93, 0.009954658163645555),
(27, 0.009952643866162018),
(47, 0.009952643866162018),
(53, 0.009952643866162018),
(73, 0.009952643866162018),
(43, 0.00995062956867848),
(33, 0.009934515188810174),
(67, 0.009934515188810174),
(13, 0.009864014776886339),
(37, 0.009864014776886339),
(63, 0.009864014776886339),
(87, 0.009864014776886339),
(0, 0.005853548487161875),
(100, 0.005853548487161875)
При такой генерации доля чисел, кратных 5, составляет

(99968 из 496451).