Роль интуиции, догадки в решении задач

[vadimm]

Еще раз убедился, что у меня отвратительно получается догадываться до ключевых моментов в задачах. То есть догадаться я так и не могу, сдаюсь и лезу за подсказками. Насколько важен этот навык? А если у меня нет этого, какой-то сверхинтуиции, что делать - прекращать учить?

Вот пример. Нужно было доказать, что если в группе для любого элемента справедливо $aa=e$, то группа абелева. Я примерно час крутил-вертел элементы группы и в итоге не смог прийти к осмысленному ответу и поднял белый флаг. Полез за подсказкой. Выяснилось, что нужно было рассмотреть $(bc)(bc) = e$. Далее все понтяно.

Хммм. Это вообще как понимать? Как нормальный человек должен догадаться до такой идеи, как? Мне то нормальной казалось идея рассмотреть $ab$ и $ba$ и домножать их слева, справа на элементы $a$ или $b$, в надежде получить равенство $ab = ba$.

Я сильно взволнован! Что это за ерунда. Это должно быть невиданное какое-то одарение Свыше, и которое я, увы, так и не получил, чтобы мысль от посылки, что $aa=e$, вдруг резко повернула к рассмотрению $(bc)(bc)$!

[mihaild]

vadimm в сообщении #1472932 писал(а):

Как нормальный человек должен догадаться до такой идеи, как?

ИМХО тут нужно догадываться в другую сторону.
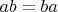
От нас хотят абелевости. Записываем, что нам нужно доказать: $ab = ba$. А дано что-то про единицу, ну давайте перепишем так, чтобы справа была единица: $a b a^{-1} b^{-1} = e$. Всё бы хорошо, но теперь обратные элементы вылезли. А вот из того, что нам дано, как раз можно и обратный элемент изготовить: $a = a^{-1}$. Подставляем, получаем, что нам нужно доказать $abab = e$. Ну а это уже можно сопоставить с тем, что дано.
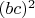
По крайней мере я рассуждал примерно так. Сразу переходить к рассмотрению $(bc)^2$ мне представляется не очень естественным.
Дальше, конечно, нужно проверить, что все переходы, которые мы делали, были эквивалентными (а не просто следствиями), и развернуть порядок рассуждения (а то мы использовали то, что нужно доказать, как посылку).

[Утундрий]

vadimm в сообщении #1472932 писал(а):

Мне то нормальной казалось идея рассмотреть $ab$ и $ba$ и домножать их слева, справа на элементы $a$ или $b$,

Ну вот почти докрутили же. Нужно было выписать все эти произведения и в одном из них наверняка заметили бы, что $abab$ это некоторым образом $(ab)(ab)$...

Или без бумажки решать пытались?

[EUgeneUS]

vadimm
Интуиция - это неосознанный опыт. Вывод: чтобы была интуиция в решении задач, нужно больше решать задач.
Так придет и осознанный опыт ("в 1800-лохматом году решал такую же", а в "1900-лохматом не точно такую же, а похожую"), и не осознанный ("похоже, тут решать надо так").

[vadimm]

Утундрий в сообщении #1472937 писал(а):

Нужно было выписать все эти произведения и в одном из них наверняка заметили бы, что $abab$ это некоторым образом $(ab)(ab)$...

Пытался и так, и так. Что-то этот момент пропустил. У меня были доможнения слева и справа на единицу: $ab = eabe = bbabaa = b(ba)(ba)a$. Но я посчитал это ошибочным и пропустил.

-- 08.07.2020, 20:28 --

EUgeneUS в сообщении #1472939 писал(а):

Интуиция - это неосознанный опыт.

Я считаю, что это больше прямой дар из чего-то трансцедентного, из мира идей что-ли. Он либо дан, либо будет мучительно больно. Ну вот было время решал я в школе, вроде успешно. Прорешал сотни задач. И как они мне помогли. Столкнулся с новым разделом математики, с новым типом задач и как мне те школьные задачи помогли? Получается никак. И что теперь, с каждым новым разделом лезть за подсказками? А задач-то не так и много. Не видел, чтобы в высшей школе давали уйму задач. Обычно дают листочек, где десяток, максимум полтора задач, причем разнотипные. Тут не разбежишься. Честно ли, почти для каждой задачи лезть в подсказки и указания, искать ответы в интернете, а не находить самостоятельно? Может быть в этом и суть математического образования, то есть к результату приходишь не сам, а просто ищешь его во всяких источниках, в той же книге или например http://math.hashcode.ru/questions/? Хотя в это и есть что-то оригинальное, разивается умение человека работать с информацией, искать её, сопоставлять, что в науке весьма полезно наверное, но не думать самостоятельно. Если мотивация другая. Научиться самому решать задачи из продвинутых курсов математики, научиться догадываться. В науку я не собираюсь лезть.

[Someone]

vadimm в сообщении #1472940 писал(а):

Я считаю, что это больше прямой дар из чего-то трансцедентного, из мира идей что-ли. Он либо дан, либо будет мучительно больно.

Неправильно считаете. Интуиция — это опыт, освоенный до такой степени, что срабатывает автоматически, на подсознательном уровне. Будете много задач решать — будет и интуиция.

[Gagarin1968]

Someone в сообщении #1472972 писал(а):

Будете много задач решать — будет и интуиция

Согласен на все 100.
Прочитайте прекрасную книгу Дж. Пойа "Математическое открытие". В ней прямо приводится методология, как подвести себя к такому озарению.

[pogulyat_vyshel]

Someone в сообщении #1472972 писал(а):

Интуиция — это опыт, освоенный до такой степени, что срабатывает автоматически, на подсознательном уровне. Будете много задач решать — будет и интуиция.

Gagarin1968 в сообщении #1473006 писал(а):

В ней прямо приводится методология, как подвести себя к такому озарению.

Если бы это все было так то в математике были бы сплошные Пуанкаре и Колмогоровы. Не имея способностей, развить интуицию трудом можно, но только до известного среднего уровня

[SomePupil]

pogulyat_vyshel в сообщении #1473008 писал(а):

Не имея способностей, развить интуицию трудом можно, но только до известного среднего уровня

Следует сказать, этот средний уровень позволяет людям решать исследовательские задачи по направлению, в котором они развивались. То есть, он (средний уровень) проходит значительно выше, чем можно было бы подумать (например, я вашу формулировку истолковал невесть как), хотя и не на уровне условного Пуанкаре, конечно.

[SergeCpp]

Цитата:

‘Как-то в беседе Хойла с Ричардом Фейнманом речь зашла об озарениях — как часто они случаются в жизни учёного. Фейнман очень ярко описал, как его осеняло, и ту эйфорию, которую он потом испытывал в течение двух-трёх дней. «И сколько раз тебя осеняло? — спросил Хойл. Ровно четыре! — не задумываясь ответил Фейнман. Мы оба пришли к выводу, что двенадцать дней эйфории не такая уж большая награда за труд всей жизни. Вообще говоря, Дику сильно повезло. Со мной такое случилось лишь однажды».’

Виталий Мацарский. Сэр Фред Хойл и драма идей, 2015.

Цитата из ЖЖ: https://evgeniirudnyi.livejournal.com/233796.html