Как всё это связано с преобразованием Фурье? Откуда всё это? Как подойти к этой теме, чтобы это понять? Пока что я вижу кучу формального материала, который не понятно к чему ведёт и, кстати, в разных учебниках написан по-разному.
Я попробовал написать, как я это понимаю, может, кому-то будет полезно.
1. Про что этоГармонический анализ занимается различными обобщениями разложения

-функций на окружности в ряд Фурье.
Я докажу аналогичный результат для произвольной компактной группы Ли вместо окружности.
Базисные функции

(на окружности, параметризованной

), по которым происходит разложение в ряд Фурье, соответствуют всевозможным неприводимым унитарным представлениям окружности, рассматриваемой как топологическая группа. Таким образом, оно задаёт разложение в гильбертову прямую сумму

, где
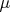
— мера Хаара на окружности (короче говоря, длина), а
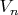
— экземпляр пространства

со стандартным скалярным произведением

и с унитарным представлением

.

само является (бесконечномерным) унитарным представлением

:

действует сдвигом аргумента на

, то есть

,

. Это представление называется
регулярным. Разложение в прямую сумму согласовано с регулярным представлением: если

, то

(доказательство:


). (Очень важно, что преобразование Фурье переводит трансляцию аргумента в умножение фурье-образа на что-то: в результате операторы дифференцирования — генераторы трансляций — под действием преобразования Фурье превращаются в алгебраические операторы. Это бывает очень полезно, например, при решении дифференциальных уравнений.)
Таким образом, регулярное представление разложилось в гильбертову прямую сумму неприводимых унитарных представлений окружности, по одному из каждого класса изоморфизма. Оказывается, подобное разложение имеет место для многих других локально компактных хаусдорфовых топологических групп. А именно, обозначим

множество классов изоморфизма унитарных конечномерных неприводимых представлений

, и выберем в каждом классе

представление

(группа унитарных операторов на

). Тогда во многих случаях можно построить разложение в прямой интеграл

, где
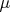
— мера Хаара на

, а интеграл берётся по какой-то мере на

.
- Если
 компактна и абелева, то это просто считающая мера, все неприводимые представления одномерны, и прямой интеграл сводится к гильбертовой прямой сумме, как в классическом случае окружности.
компактна и абелева, то это просто считающая мера, все неприводимые представления одномерны, и прямой интеграл сводится к гильбертовой прямой сумме, как в классическом случае окружности. - Если она компактна, но не абелева, то всё то же самое, но неприводимые представления не обязательно одномерны.
- Если группа абелева, но не компактна (а только локально компактна), то интеграл к прямой сумме уже не сводится. Однако в этом случае (как и в случае 1)
 само естественным образом является локально компактной абелевой хаусдорфовой топологической группой (умножение происходит из операции тензорного умножения предствлений), и прямой интеграл берётся по её мере Хаара. Сопоставление топологических групп
само естественным образом является локально компактной абелевой хаусдорфовой топологической группой (умножение происходит из операции тензорного умножения предствлений), и прямой интеграл берётся по её мере Хаара. Сопоставление топологических групп  называется двойственностью Понтрягина. Классический частный случай —
называется двойственностью Понтрягина. Классический частный случай —  : это преобразование Фурье. (
: это преобразование Фурье. ( .)
.)  неабелева и некомпактна. Это самый сложный случай, и он до конца не понят. Разложение в прямой интеграл вышеуказанного вида доказано, например, для всех вещественных (или комплексных) алгебраических редуктивных групп. Например, для
неабелева и некомпактна. Это самый сложный случай, и он до конца не понят. Разложение в прямой интеграл вышеуказанного вида доказано, например, для всех вещественных (или комплексных) алгебраических редуктивных групп. Например, для  .
.
Далее мы сосредоточимся на компактных группах, то есть на случае 2 (случай 1 туда тоже будет включён). В этом случае

«дискретно» (нестрогое утверждение), поэтому сложного анализа не будет (в частности, прямых интегралов не будет и знать про них ничего не надо).
2. Обозначения, соглашения(В предыдущем пункте обозначения были немного другие, смотрите сюда, а не туда.)

— компактная группа Ли.
- Cвязность не предполагается. То есть конечные группы сюда входят как частный случай (дискретная топология превращает конечную группу в
 -мерную группу Ли).
-мерную группу Ли).
- Предположение о гладкости не очень существенно: почти всё следующее верно для произвольной компактной хаусдорфовой топологической группы.
- Предположение о компактности очень существенно.

— множество классов изоморфизма неприводимых конечномерных комплексных непрерывных представлений

.
(Оффтоп)
Далее мы увидим, что мы ничего не потеряли бы и не приобрели, если бы рассматривали классы изоморфизма унитарных представлений на эрмитовых пространствах.
Мы будем считать, что в каждом классе

выбрано определённое представление

на комплексном векторном пространстве

(от этого выбора мало что зависит).
Все представления по умолчанию предполагаются комплексными и непрерывными.
Если

— векторное пространство, то

— двойственное векторное пространство. Эрмитово скалярное произведение линейно по первому аргументу.
Я не различаю элементы пространства

(классы функций по отношению эквивалентности «совпадают вне множества нулевой меры») и сами эти функции, но ничего плохого от этого не случается.
Вейлем везде называется Герман Вейль.
3. Лемма ШураПусть

и

два представления.
Морфизмом представлений 
называется линейное отображение
 (сплетающий оператор)
(сплетающий оператор), коммутирующее с представлениями, то есть для любого

должно быть

.
Лемма Шура. Если

— конечномерное неприводимое представление

, то все морфизмы

пропорциональны тождественному. Если

и
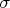
— неизоморфные конечномерные неприводимые представления, то между ними есть только нулевой морфизм.
Доказательство: Пусть

сплетающий оператор. Его ядро и образ

-инвариантны; так как

и
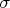
неприводимы, то они либо

, либо всё пространство. Это значит, что либо

, либо он биективен, то есть является изоморфизмом представлений.
Если

, то рассмотрим его собственное значение

оператора

. Для

верно всё, что выше написано про

, но биективным он быть уже не может, значит, он нулевой, то есть

.
 4. Мера Хаара
4. Мера ХаараВ этом пункте мы будем существенно использовать предположение, что

— группа Ли. Мера Хаара определена и для произвольной (локально) компактной хаусдорфовой топологической группы, но эта ситуация несколько сложнее (а если группа некомпактна, то мер Хаара две: левая и правая, они могут не совпадать).
Обозначим

отображение левого умножения на

, то есть

. Аналогично

— отображение правого умножения.
Предложение. Любая группа Ли ориентируема. Зафиксируем на нашей компактной группе Ли

одну из двух возможных ориентаций. Тогда есть единственная дифференциальная форма

старшей степени на

со следующими свойствами:
- Инвариантность относительно левого умножения:
 для любого
для любого  .
.  .
.
(Естественно, можно заменить в формулировке левое на правое.)
Доказательство: Это простое применение некоторых стандартных фактов теории групп Ли, которые я сейчас напомню.
Любой вектор из касательного пространства к единице группы можно разнести левым (а можно и правым) умножением на всю группу и получить таким образом левоинвариантное векторное поле на группе. Подробнее: пусть

, тогда положим

. Это векторное поле левоинвариантно:

, и оно не обращается в 0 при

, так как

— диффеоморфизм. Поэтому полученное отображение

— послойный изоморфизм. Оно гладко, потому что оно есть композиция гладких отображений

, где первая стрелка индуцирована вложением

, вторая — нулевым сечением

, а последняя — дифференциал гладкого отображения умножения

. Таким образом, все левоинвариантные векторные поля гладкие, и мы построили тривиализацию касательного расслоения

.
(Оффтоп)
Чтобы доказать изоморфность локально тривиальных гладких векторных расслоений, достаточно построить гладкий послойный изоморфизм между ними: гладкость обратного отображения обеспечена локальной тривиальностью. В частности, для доказательства тривиальности достаточно построить набор глобально определённых гладких векторных полей, ограничения которых на касательное пространство к каждой точке базы составляют там базис.
Теперь можно брать двойственные расслоения, тензорные степени и т. д.; в частности, получается изоморфизм

(влекущий ориентируемость

). Соответствующее отображение

переводит форму

в её левоинвариантное продолжение — форму

— и устанавливает изоморфизм

и пространства левоинвариантнах дифференциальных форм старшей степени на

.
Выберем там произвольную

и положим

. (

конечен в силу компактности

и не равен нулю, так как в силу левоинвариантности

ни в одной точке

не обращается в 0.) Так как пространство левоинвариантных форм старшей степени 1-мерно (в силу вышеуказанного изоморфизма), то

есть единственная левоинвариантная форма с интегралом 1.
 Предложение.
Предложение. Эта форма инвариантна и отностельно правого умножения тоже.
Доказательство: Заметим сначала, что для любого

форма

левоинвариантна (так как левое и правое умножение коммутируют, то и их обратные образы коммутируют:

.) Поэтому

, где

— так называемая
модулярная функция. Она гладкая (частное ненулевых гладких функций). Более того, это гомоморфизм групп (

), поэтому её образ — подгруппа

по умножению. Так как

компактна, а

непрерывна, то образ

компактен. Однако в группе

по умножению нет нетривиальных компактных подгрупп. Действительно, она топологически изоморфна
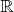
по сложению (изоморфизм — логарифм), в
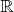
компактность равносильна ограниченности, а любой ненулевой

аддитивно порождает неограниченную подгруппу. Итак, для компактной группы модулярная функция тождественно равна единице.

Порождаемая этой формой мера называется
мера Хаара; интеграл от функции

по этой мере мы будем обозначать

, а соответствующее

-пространство —

.
Замечание. Из существования ненулевой биинвариантной формы старшей степени

можно вывести существование биинвариантной
римановой метрики на компактной группе Ли

(относительно которой

будет формой объёма). Но такая метрика не единственна, если

не проста.
5. Унитаризуемость конечномерных представлений компактных группПредложение. Пусть

конечномерное представление

. Тогда можно выбрать эрмитово скалярное произведение на

так, что все операторы

(

) будут относительно него унитарны. Если

неприводимо, то такое скалярное произведение единственно с точностью до масштабирования (домножения на ненулевое комплексное число).
Доказательство: Выберем любое эрмитово скалярное произведение

на

и усредним по группе:

. Полученное является эрмитовым скалярным произведением, и для любого

верно

, то есть все операторы представления унитарны.
Единственность следует из леммы Шура (упражнение).
 Предложение.
Предложение. Любое унитарное конечномерное представление

раскладывается в прямую сумму неприводимых подпредставлений.
Доказательство: Пусть

— нетривиальное

-инвариантное подпространство, тогда

тоже: если

, то для любого

и

имеем

, поэтому

. Мы разложили

в нетривиальную прямую сумму

, дальше будем делать то же самое со слагаемыми, и через конечное число шагов получим прямую сумму, все слагаемые которой неприводимы (потому что размерность

конечна).
 Следствие.
Следствие. Любое конечномерное представление компактной группы Ли раскладывается в прямую сумму неприводимых.
 Замечание.
Замечание. Для некомпактных групп это может быть неверно: например, представление

,

не раскладывается в прямую сумму неприводимых.
6. Представляющие функцииПусть

— конечномерное представление

.
Каждому линейному функционалу

на пространстве

линейных операторов

соответствует (непрерывная) комплекснозначная функция

на

. Такие функции называются
представляющие функции представления

. Они образуют конечномерное подпространство в пространстве

всех непрерывных функций на

— образ вышеописанного (линейного) отображения

.
Это подпространство не меняется при замене

на изоморфное представление

, потому что представляющие функции

выражаются
линейно через представлящие функции

:

.
Представляющие функции, соответствующие функционалам вида

(

), называются
матричные элементы представления

. Так как

линейно порождается функционалами указанного вида, то пространство представляющих функций данного представления линейно порождается его матричными элементами.
7. Скалярное произведение Фробениуса (напоминание из линейной алгебры)Пусть

комплексное векторное пространство с эрмитовым скалярным произведением. Тогда

линейно порождается операторами вида

(

), и это задаёт естественный линейный изоморфизм

. Он позволяет нам определить эрмитово скалярное произведение на

: для разложимых тензоров положим

, и продолжим на всё пространство по полуторалинейности. (Это стандартное определение тензорного произведения гильбертовых пространств; если размерности бесконечны, то ещё надо пополнить.) Полученное эрмитово скалярное произведение на

называется скалярное произведение Фробениуса; будем обозначать его

. Если

— ортонормированный базис

, то

.
Как обычно, скалярное произведение на

определяет скаляное произведение на

, его мы будем обозначать так же.
Если

является пространством неприводимого конечномерного представления

, то, как мы помним, на

есть единственное с точностью до масштабирования скалярное произведение, относительно которого представление унитарно. Скалярное произведение Фробениуса не меняется при масштабировании скалярного произведения на

(упражнение), то есть оно
однозначно определяется представлением.
Нам будет удобно перемасштабировать его следующим образом: для

мы полагаем

. (Эквивалентно, для


.)
8. Cоотношения ортогональностиЛемма. Пусть

и

конечномерные представления,

— линейное отображение. Тогда его усреднение

— сплетающий оператор. Если

, то

.
Из этого утверждения и из леммы Шура сразу следует, что если

и
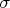
неприводимы, то
 Доказательство:
Доказательство: 
.
Если

, то

.
 Теорема (соотношения ортогональности).
Теорема (соотношения ортогональности). Представляющие функции неизоморфных
неприводимых конечномерных представлений

ортогональны в

.
Если

неприводимое конечномерное представление,

, то

скалярное произведение соответствующих представляющих функций

(скалярное произведение Фробениуса, делённое на

; см. выше).
(В более явном виде это значит, что если выбрать на

эрмитово скалярное произведение, относительно которого

унитарно, и выбрать ортонормированный базис

относительно этого скалярного произведения, то в этом базисе будет

, если

и

, а иначе

.)
Доказательство: Достаточно проверить равенство для матричных элементов, потому что они порождают пространство представляющих функций.
Зафиксируем на

и

эрмитовы скалярные произведения, относительно которых представления унитарны. Тогда любой матричный элемент

равен

для каких-то

, и аналогично любой матричный элемент
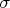
равен

для каких-то

.
Итак, надо доказать, что для любых

верно

Нужное нам ревенство получается применением предыдущей леммы к оператору

,

:

скалярное произведение наших матричных элементов есть в точности

, причём при

след

.
(Удобнее всего это считать в обозначениях Дирака: вектор

обозначается

, скалярное произведение

,

. В этих обозначениях

, поэтому оператор

в них записывается

, и сразу видно

.)
 9. Теорема Петера — ВейляТеорема.
9. Теорема Петера — ВейляТеорема. Линейная оболочка множества матричных элементов конечномерных неприводимых представлений плотна в пространстве

непрерывных функций на

(с нормой

).
(Отсюда следует, что она плотна и в

, так как

плотно в

, а вложение

непрерывно.)
Доказательство (простая часть): Слово «неприводимых» из формулировки можно убрать, потому что любое конечномерное представление раскладывается в прямую сумму неприводимых (и, значит, любой матричный элемент конечномерного представления — сумма матричных элементов неприводимых конечномерных представлений).
Линейная оболочка множества матричных элементов всех конечномерных представлений образует унитальную

-подалгебру в

, потому что:
- произведение матричных элементов 2 представлений — матричный элемент тензорного произведения этих представлений,
- функция, комплексно сопряжённая к матричному элементу — матричный элемент комплексно сопряжённого представления,
- функция, тождественно равная единице — матричный элемент тривиального 1-мерного представления.
По теореме Стоуна — Вейерштрасса, осталось доказать, что матричные элементы конечномерных представлений разделяют элементы

, то есть что для любых

найдётся конечномерное представление

, такое что

; равносильное утверждение: для любого

найдётся

, такое что

.
Для конечной группы

это очевидно: подойдёт регулярное представление. Это также очевидно в случае когда

матричная группа Ли, то есть замкнутая подгруппа

. Так что для этих случаев доказательство здесь заканчивается.

Вообще-то любая компактная группа Ли матричная, так что хотелось бы на этом совсем закончить. Но доказать это — примерно всё равно, что доказать теорему Петера — Вейля без предположения о матричности. Поэтому всё равно приходится продолжить.
10. Доказательство в общем случаеЧтобы доказать теорему Петера — Вейля в общем случае, осталось доказать следующее: пусть

компактная группа Ли,

, тогда найдётся конечномерное представление

группы

, такое что

.
Сначала нужна некоторая подготовка.
10.1. ТрансляцииПусть

,

. Тогда функция

тоже из

(это композиция измеримых отображений — несложно показать, что непрерывные отображения топологических пространств измеримы относительно борелевских
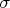
-алгебр, — а интеграл квадрата её модуля равен

в силу инвариантности меры Хаара). Таким образом, определён унитарный (в частности, непрерывный) линейный
оператор левой трансляции 
.
Непрсредственно проверяется, что

, так что операторы левой трансляции образуют унитарное представление

; оно называется
левое регулярное представление.
То же самое можно сказать про операторы правой трансляции

: они образуют правое регулярное представление.
10.2. Интегральные операторы (напоминание)Пусть

и

— пространства с
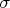
-конечными мерами,

. Тогда определён
интегральный оператор с ядром 
, который

превращает в функцию

на

. Из функционального анализа известно, что эта формула корректно определяет непрерывный линейный оператор

, причём он компактен.
10.3. СвёрткиПусть

. Определим функцию

—
свёртку 
и

.
Правая (для определённости) свёртка с фиксированной функцией

— интегральный оператор

c ядром

. Оно измеримо (композиция измеримых функций) и принадлежит

— это следует из теоремы Фубини и из конечности меры Хаара на компактной группе:

. Поэтому свёртка любых функций из

принадлежит

(на самом деле она даже непрерывна, но это сейчас не важно), а
оператор правой свёртки 
непрерывен и компактен.
Прямая проверка показывает, что если для любого

верно

, то

симметричен, следовательно самосопряжён.
Прямая проверка показывает, что операторы правой свёртки коммутируют с левыми трансляциями.
Всё это можно повторить и про операторы левой свёртки

(только они коммутируют с правыми трансляциями).
10.4. Окончание доказательства теоремы Петера — ВейляИтак, предположим, что

,

, но

для любого конечномерного представления

. В частности, это верно для любого конечномерного подпространства

, инвариантного относительно левых (или правых) трансляций.
Пусть

какая-нибудь функция, такая что

(это условие, обеспечивающее самоспряжённость оператора

правой свёртки с

). Спектральная теорема в применении к

даёт разложение в гильбертову прямую сумму ортогональных подпространств

, где

пробегает собственные значения

, а

означает соответствующее собственное подпространство. Так как

самосопряжён, то все его собственные значения вещественны, а так как он компактен, то единственная допустимая предельная точка множества собственных значений —

, причём при


обязательно конечномерно.
Так как правые свёртки коммутируют с левыми трансляциями, то для любого

подпространство

инвариантно относительно левых трансляций:

влечёт

для любого

. Значит,

(где

— нехороший элемент, зафиксированный нами в начале) действует тождественно на любом конечномерном

, то есть на любом, кроме, может быть,

. Поэтому

, то есть

. То есть

для любой

.
Если

, то так быть не может. Действительно, выберем окрестность

единицы, так чтобы

и

(это можно сделать в силу хаусдорфовости

и непрерывности операций умножения и взятия обратного). Теперь пусть
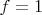
на

и

вне её.
Тогда

(потому что

и


), а

.
 11. Ряды Фурье
11. Ряды ФурьеИз ортогональности матричных элементов неизоморфных представлений следует, что множество

классов изоморфизма неприводимых представлений

не более чем счётно. Теперь из теоремы Петера — Вейля следует, что оно конечно, если

конечна, и счётно, если бесконечна.
Мы установили, что для любого

взятие матричного элемента

есть изометрическое вложение (это соотношения ортогональности для одного неприводимого представления). Продолжим это до

,

(последняя формула называется
формула обращения Фурье); это тоже изометрическое вложение (в силу соотношений ортогональности для неизоморфных неприводимых представлений) с плотным образом (по теореме Петера — Вейля). Поэтому его продолжение на пополнение

— гильбертову прямую сумму

— задаёт изоморфизм гильбертовых пространств

. Обратный к нему изоморфизм

называется
преобразование Фурье. На непрерывных функциях

оно задаётся формулой

.
Разложение функций на окружности в ряд Фурье соответствует

: если присвоить номер

неприводимому представлению

, то последняя формула сводится к интегральной формуле для коэффициентов Фурье, а формула обращения Фурье делает ряд Фурье из совокупности коэффициентов Фурье.
Конечно, можно выбрать в каждом

эрмитово скалярное произведение, относительно которого представление

унитарно, и ортонормированный базис относительно этого скалярного произведения, и записывать

и

, чтобы было совсем похоже на формулы классической теории рядов Фурье.
12. Разложение регулярного представленияВпрочем, интересно здесь не существование изоморфизма гильбертовых пространств (любые 2 бесконечномерные сеперабельные гильбертовы пространства изоморфны), а то, что он задаёт изоморфизм представлений.
А именно, вспомним, что на

есть 2 унитарных представления группы

:
левое регулярное 
и
правое регулярное 
; таким образом, на

имеется
регулярное представление группы

(первый множитель действует левым регулярным представлением, а второй правым). На

тоже есть 2 представления

: левое домножение

и правое домножение

(соответствующее представление

на

есть не что иное как
внешнее тензорное произведение 
).
Так вот, преобразование Фурье коммутирует с указанными представлениями

и поэтому задаёт изоморфизм регулярного представления

на

и гильбертовой прямой суммы представлений

.
В частности, рассматривая действие только первого множителя

, получаем, что левое регулярное представление

на

изоморфно гильбертовой прямой сумме

. То есть оно содержит в качестве прямого слагаемого каждое конечномерное неприводимое представление, столько раз, какова его размерность.



