Доброго времени суток!
Условие задачи: Пусть
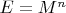
- комплексное евклидово пространство

-матриц ( с комплексными элементами ) со скалярным произведением

. Пусть

- подпространство матриц с нулевым следом. Найдите ортогональное дополнение к F.
Очевидно, что размерность

, а значит размерность ортогонального дополнения равняется

.
Каждый элемент ортогонального дополнения ортогонален элементу из

, т.е. их скалярное произведение равно нулю.
Пусть матрица

, а
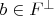
. Тогда их скалярное произведение будет равно
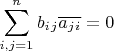
Что делать дальше?..