У второй матрицы на диагонали нет единицы.
Да, согласен -- я писал с мобильного устройства и не проверил. Нужно было так:

и

.
Вы иммете ввиду размерности собственных подпространств?
Да. В бесконечномерном случае это называется "кратность спектра" или "функция кратности спектра". В Вашем примере именно она и различается.
Но я не знаю простого строго объяснения. Полное доказательство есть в книге Бирман, Соломяк "Спектральная теория самосопряжённых операторов в гильбертовом пространстве".
Можно, например, на языке циклических векторов. Для первого оператора (назовём его

) существуют два вектора

, такие, что множество линейных комбинаций векторов
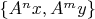
плотно в гильбертовом пространстве. Это означает, что его кратность спектра не выше 2. Если бы было достаточно одного вектора, кратность была бы равна одному.
Для второго оператора такой пары векторов не существует. Минимальный набор векторов будет счётным. Другими словами, кратность спектра равна бесконечности.
Но строить эти вектора руками -- то ещё удовольствие.
-- Пт, 29 май 2020 15:58:08 --Точнее, строить как раз легко, но не очень легко доказывать.