Здравствуйте, хотел бы проверить правильность своих рассуждений.
Даны
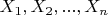
- независимые случайные величины.

. Нужно показать, что

является мартингалом относительно сигма-алгебры

.
Нужно показать выполнения трёх свойств:
1 . Существование матожидания. Матожидание процесса

существует и равно нулю, так как по свойствам матожидание суммы равно сумме матожиданий, а величины в произведениях независимы, соответственно матожидание произведения равно произведению матожиданий. И это всё равно нулю, поскольку матожидание каждой с.в. нулевое.
2. Измеримость.

измерим относительно сигма-алгебры

, поскольку состоит из линейной комбинации случайных величин, её порождающих.
3. Нужно показать, что

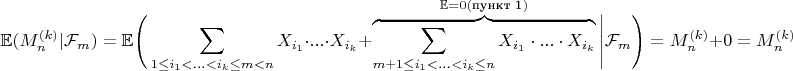
И получим, что процесс

- мартингал. Правильно всё?