Спасибо, посмотрел. Мне непонятно, почему нелинейный интегральный оператор в правой части уравнения удовлетворяет условиям этой общей теоремы, т.е. некоторая его степень является сжатием. Одна из трудностей состоит в вычетаемой постоянной

.
Ну вот как бы этот вопрос относительно простой. Нужно доказать, что

для любых точек нашего пространства. Соответственно, рассмотрев

с помощью последовательных неравенств этот переход осуществляется (
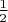
сразу же исчезает с горизонта).
-- 21.05.2020, 17:22 --Тогда - все правильно: лучшую константу (годную везде) и не получить. Так что придется работать именно с ней (я полагаю, это от Вас и желают)
А если не секрет, почему вы думаете, что лучшую константу не получить?
Хотя, наверное, на самом деле в каждом переходе можно придумать такие хитрые функции, в которых будет типа строгое равенство или что-то в таком духе... но мне сложно утверждать это однозначно.