Пусть

некоторое натуральное число и дан набор соответствий:

, где все

.
Задача состоит в том, чтобы выбрать перестановку

элементов из числа всех допустимых перестановок случайным образом (вероятность каждой допустимой перестановки должна быть одинаковой). Перестановка

является допустимой, если для любого

верно, что

Иными словами, допустимая перестановка не должна переводить элемент в элемент соответствующего множества. Существование хотя бы одной допустимой перестановки гарантируется.
Идея:
1. Построить двудольный граф с

элементами в каждой из долей
2. Соединить каждую вершину

из левой доли со всеми вершинами из правой доли, которые не принадлежат множеству
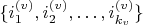
.
3. Присвоить каждому ребру в графе вес, независимо сгенерированный из равномерного распределения на отрезке
![$[0, 1]$ $[0, 1]$](https://dxdy-03.korotkov.co.uk/f/e/8/8/e88c070a4a52572ef1d5792a341c090082.png)
4. Найти полное паросочетание максимального веса
Верно ли, что соответствующая перестановка удовлетворяет условию задачи, то есть выбрана случайным образом (равномерно) из всех допустимых перестановок? Кажется, что да, так как из соображений симметрии непонятно, почему какая-то допустимая перестановка должна иметь большую вероятность, чем другие. Но формально показать не получается.



