Hi guys,
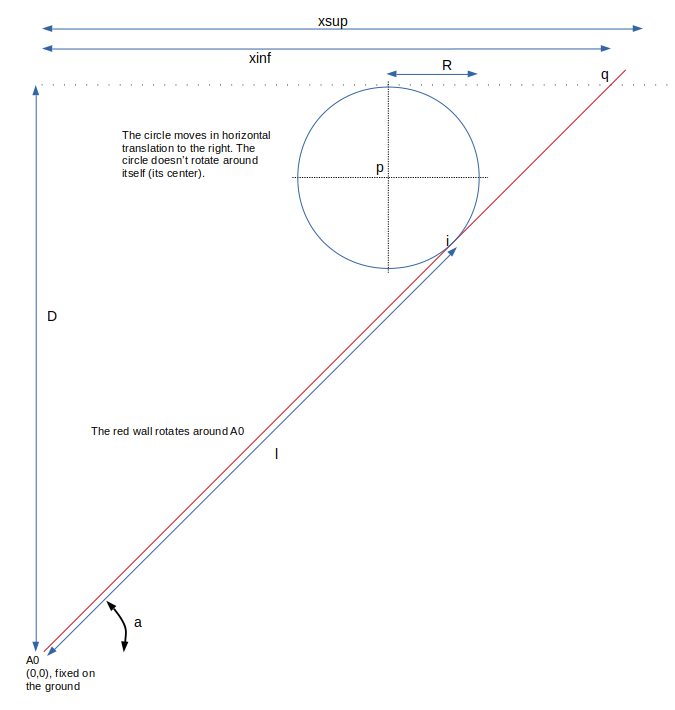
A circle moves in horizontal translation, the circle doesn't rotate around itself. A red wall is always in contact with the circle. That red wall is in rotation around the axis of rotation
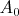
. The axis
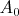
is fixed to the ground. For that, I have two external devices : a hydraulic cylinder and an electric motor for example that control the circle and the wall in position. The circle is always in contact with the wall (the hydraulic cylinder and the motor do it). I consider the device with a mass very low and there is no acceleration/deceleration just to simplify the calculations. All the perfectly bodies are rigid except the elastic. I consider the force of the elastic constant at

. I study the sum of energy between a start position (the red wall at
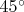
relatively to the horizontal) and a final position
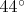
. It is enough to measure something and have enough accuracy with the drawings. But I wrote the numerical integral to verify what I measured.
I drew the device:
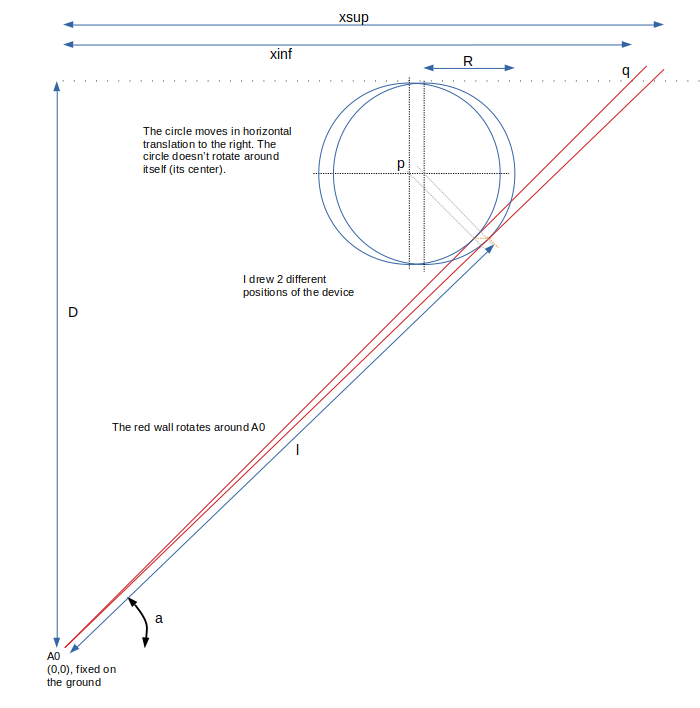
I drew two positions of the device, note the circle doesn't rotate around istelf:
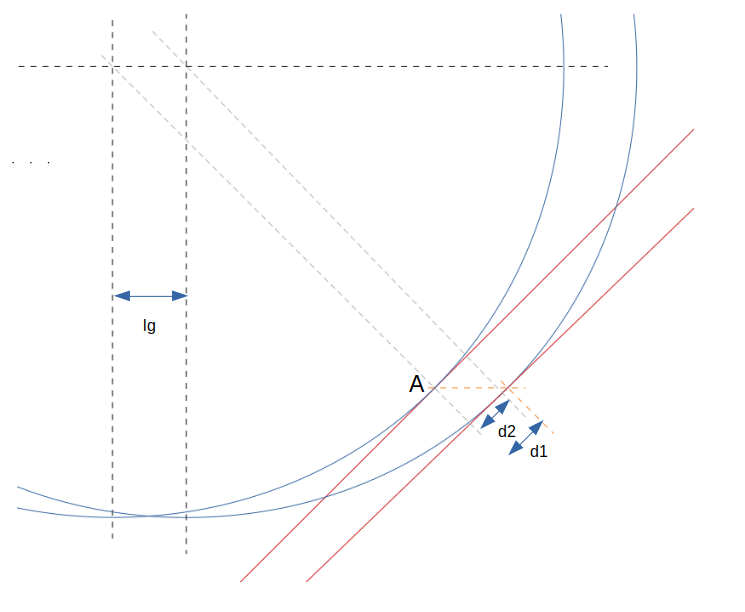
I show an enlargement of the device:
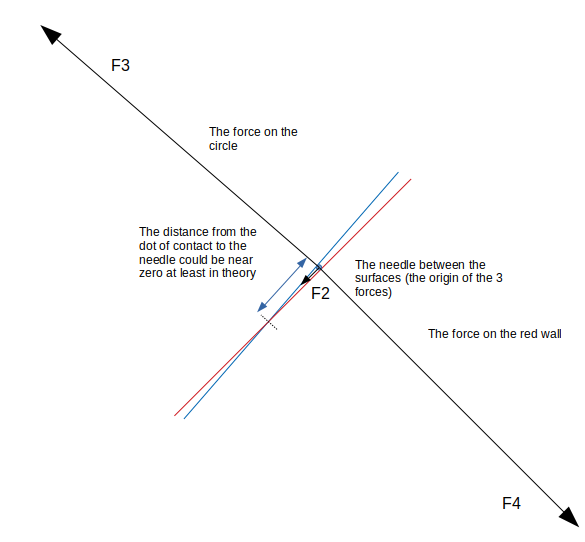
And I place a needle, very thin, in theory the diameter of the needle is one atom, between the two surfaces of the circle and the wall.The needle cannot be at the exactly dot of contact but the distance from it can be very small:
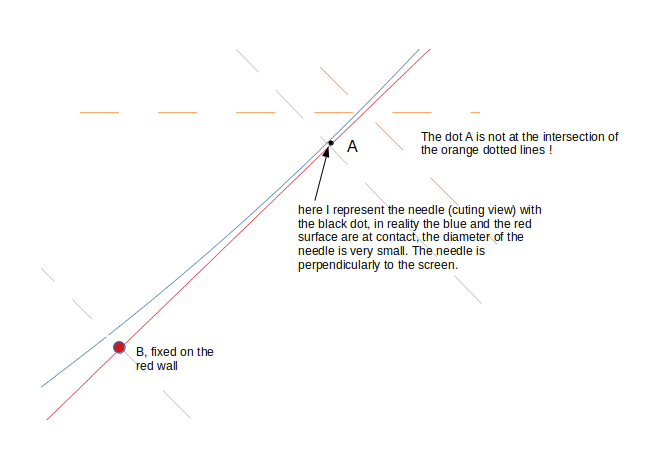
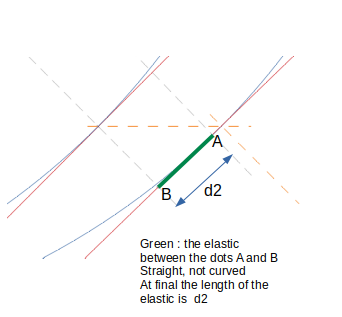
I place two dots on the device, the dot

fixed on the wall and the dot

fixed on the needle. At start, the dots

and

coincide and at final they represent the length of the elastic:

Note, the needle is blocked by the surfaces of the circle and the wall because I have an elastic between the dots

and

, this is the forces that I drew:
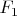
and
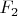
, and I represent the elastic by a small green line, the elastic is straight not curved:
I drew the forces from the needle on the surfaces of the circle and the wall, note if the diameter of the needle is very small the distance of the needle from the dot of contact is near zero:
At start, the length of the elastic is zero and at final it is
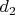
, so the energy stored inside the elastic from start to end is
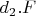
. I need an energy to move the circle it is
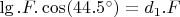
. The forces
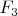
needs the same work I recover from
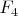
: I measured the lengths but I also compute the energies for
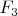
and
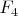
. I can give the numerical integral if you ask. So the sum of energy is
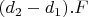
and it is not normal.
So my question is: have you an idea where is my mistake ?



