Численная траектория выходит на стационарный режим.

[Lorein_]

Доброго времени суток.
Помогите разобраться в вопросе. Есть система из трёх ОДУ первого порядка, нужно численно решить её используя счёт на установление. То есть поставлено условие [x_{0},+\infty). Точки
вычисляют до тех пор, пока численная траектория не выйдет на стационарный или
периодический режим и (или) до тех пор, пока счет не будет остановлен пользователем
(например, потому, что траектория «уходит в бесконечность»).
Я пишу программу для численного решения этой системы. Вопрос состоит в том какое условие нужно проверять для остановки счёта?

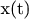
Стационарное состояние, например, для автономной системы из двух уравнений можно определить как значения функций x(t) и y(t), удовлетворяющие системе алгебраических уравнений:

$$\left\{ \begin{array}{rcl} P(x,y)=0 \\ Q(x,y)=0 \\ \end{array} \right.$$

То есть для остановки счёта для системы из двух уравнений нужно проверить условие, что текущая точка удовлетворяет системе выше?

[Pphantom]

Lorein_ в сообщении #1461227 писал(а):

Вопрос состоит в том какое условие нужно проверять для остановки счёта?

А вы уверены, что этим набор вариантов исчерпывается (ну, само собой, кроме принудительной остановки)? Например, аттрактор Лоренца возникает в системе трех ОДУ первого порядка. Соответственно, при вычислениях с конечной точностью для него можно получить номинально "периодический" режим, который таким на самом деле не является. При этом проверка периодичности будет безумно ресурсоемкой, а если огрубить результаты - бесполезной.

Так что, по-видимому, условие остановки стоит формулировать, исходя из смысла задачи, в общем случае ничего хорошего не получится.

[Lorein_]

Pphantom в сообщении #1461232 писал(а):

Так что, по-видимому, условие остановки стоит формулировать, исходя из смысла задачи, в общем случае ничего хорошего не получится.

В моём случае система описывает модель биологического сообщества хищник и две жертвы. Нужно исследовать поведение траекторий системы при двух фиксированных наборах параметров(устойчивое и неустойчивое равновесное состояние)

[Pphantom]

Мда. Тогда я бы сначала посмотрел на получающиеся результаты при разных значениях параметров, а уже потом выбирал метод остановки.

Это если подобное вообще имеет смысл - на практике для такой задачи проще насчитать модель с гарантированным запасом, чем возиться с критерием остановки счета.