Но, возможно, в ответе требуется указать, как именно устроен каждый из них
Ну как устроены гомоморфизмы я, вроде, представляю (кратные НОД идут в ноль, (кратные НОД + 1) идут в

и т.д.). Это ведь имеется ввиду?
По поводу неприводимых.

Производная - неприводимый многочлен. Значит, исходный многочлен не имеет кратных корней. Тогда

не имеет корней. То есть представление размерности

разлагается в сумму одномерных в количестве

и неприводимое размерности
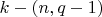
. Наверное, что-то не так? Верной ли хоть дорогой иду?



