Присоединяюсь.
Вообще, чел, изучивший вариационное исчисление (я просмотрел историю сообщений ТС), вроде бы, не должен путаться в таких простеньких вещах (и называть Эр-2 "квадрат множества вещественных чисел"). Как то это мне все сомнительно - так что я выхожу из дискуссии...
Вот давайте не будем считать кто что должен и чего не должен. Вы, например, путаете задание функции с заданием её области определения, а я потом должен расшифровывать, что Вы сказать хотели. Вам кажется это элементарным, а я Вас понять не могу.
область определения у

-

.
Нет.
С этой

, вот цитирую:
Пусть

,

- линейное (задается матрицей). Вместо

будем рассматривать пространство

линейных отображений из

в

(его, кстати, называют сопряженным к

), его элементами будем считать вектора из

, (т.е., каждое

определяется неким вектором

, и действует по правилу

- здесь - скалярное произведение). Вот. И что тогда есть
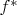
?
На каком множестве она определена? Она является элементом

? Значит она определена на

, почему нет?
-- 24.04.2020, 23:37 --Остальным спасибо, вопрос, в принципе, исчерпан. Тема возникла из - за того, что меня очень удивило слово "сопряжение" по отношению к разным по абстрактности элементам, но, я понял, что это удивляет не только меня. Употребление этого слова не-очень-то-и-строгое, и сопряжения бывают разные.
Если
DeBill соберётся с силами и напишет опрятно, что он мне хотел сказать, я с удовольствием послушаю и буду решать его примеры. Какие там плоскости в двухэлементных множествах, почему они не, например, отрезки?