Ой, ужас, эта книга вроде уже кого-то в сторону от нормального простого тензорного исчисления увела здесь на форуме.
А точка — и скалярное произведение, и применение оператора к вектору? Тогда уже даже непонятно, откуда берётся

(справа видимо скобки вокруг
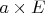
?), ведь векторное произведение определено только для векторов, нельзя векторно умножить на

. Или если в книге это доопределяется, то скажите, как именно. Хотя целиком результат

верен. И второй дальше тоже, а вот вывод
из чего имеем

.
сомнительный. Точно доказано, что можно сокращать, даже если один из аргументов

? По-моему нельзя получить даже

.