waxtep, придумал. Сначала посчитаем все купюры ценностью от 1 у.е. до 99 у.е., в каждой сотне их будет 99 штук, а количество сотен легко подсчитать. Получим
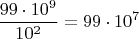
купюр. Далее, займёмся сотенными купюрами. В промежутке от 100 у.е. до 199 у.е. содержится 100 сотенных купюр. Таким образом, подсчитаем все сотенные купюры, которые нужны, чтобы составить числа от 100 до

. К ним прибавляем сотенные купюры, составляющие в сумме миллиард.

. Допустим, что все купюры одинаковой массы 1 г. Далее, сложив всё это хозяйство, можно оценить массу, если я всё правильно подсчитал. Проверьте меня, пожалуйста, может быть где-то не так рассуждаю.
-- 22.04.2020, 20:10 --Someone, спасибо, но я интересовался этим вопросом: "Попробуйте оценить также массу бумаги, предполагая, что использованы не более чем сотенные купюры." Я плохо выделил, видимо, в теме вопрос. Вроде бы уже решил, проверьте, если несложно, не наврал ли я где.



