Unmensch
1) Кто сказал, что решение неверное?
2) Что именно неверно - решение или ответ?
1) Да я пытался устроиться на онлайн-подработку, это было одно из тестовых заданий :) Мне просто сообщили после проверки, что неверно это и ещё одно, которое чуть позже тоже выложу :)
2) Было указано, что просто неверно сделано, при этом не было уточнено, решение или ответ.
Тогда к концу дня выполнится ровно одно из следующих событий:
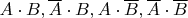
А зачем вы события перемножаете, а не вероятности?
(Оффтоп)
Такой ответ: 0,6312?
Потому что произведение событий двух событий это событие, при котором происходят оба события, или что Вы имели в виду?
А ответ я не знаю какой :) А как Вы считали?
Вероятность того, что в одной из стоек в течении рабочего дня закончится бумага, равна 0,16
Это вероятность того, что бумага закончится хотя бы на одной стойке, ровно на одной стойке, или на данной стойке?
Да вот не уточнено.
Вероятность того, что в одной из стоек в течении рабочего дня закончится бумага, равна 0,16.
Вот это условие сформулировано недостаточно ясно.
Хотя бы в одной стойке? Тогда решать нечего, условия избыточны, искомая вероятность равна

.
Только в одной? Тогда Ваше решение правильно.
Возможно, имелось в виду, что вероятность того, что бумага закончится в первой стойке, равна
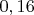
?
Да, может и так, действительно, не очень ясная формулировка.