Well a friend of mine just found the optimal for ^16. First this gave me some hope. But then he said that it was a massive effort for him and he is one of the best marathoners at TopCoder, so all my hopes were completely destroyed...
Speaking of TopCoder, I frequently write problems for their long competitions (1 week). They are really fun and competitive! So I invite you all to participate. The next one is on 22nd April.
-- 08.04.2020, 16:26 --80^15=>{74,73,70,69,67,66,64,62,54,53,52,51,50,49,47,45,44,39,37,36,33,30,29,28,26,22,20,18,17,16,14,13,12,10,8,7,5,4,3,2,1}
as optimal with minimal error 2917618
Haha I did find this too, but it took me 15 minutes!
-- 08.04.2020, 16:39 --So Fermat's last theorem states that
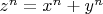
has no solutions for

. But what do we know about a more generalised version that contains more terms. We know that
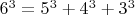
and
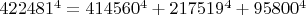
(due to Roger Frye, 1988). But does
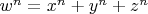
have solutions for
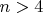
? What happens when we have more terms on the right hand side?