Наклонная плоскость, сила реакции опоры.

[profilescit]

Клин массой $M$ находится на шероховатой горизонтальной поверхности стола. Через блок, укреплённый на вершине клина, перекинута лёгкая нерастяжимая нить, связывающая грузы, массы которых $m_1$ и $m_2$ (см. рис). Грузы удерживают, затем отпускают. После этого грузы движутся, а клин покоится. Гладкая наклонная поверхность клина образует с горизонтальной плоскостью угол $\alpha$, $\sin{\alpha}=0,8$ Считайте $M =2m$, $m_1 = m $, $ m_2 =2 m $. Массой блока и трением в его оси пренебречь.
1) Найдите ускорение грузов.
2) При каких значениях коэффициента $\mu$ трения скольжения клина по столу клин будет оставаться в покое?

И вроде легкая задача, а ответ не сходится. Прошу помочь найти ошибку в рассуждениях.

Пусть $T$ сила натяжения нити.

$m_2 g - T = m_2 a$
$T - m_1 g \sin{\alpha} = m_1 a $ откуда $a = \frac{m_2 - m_1 \sin{\alpha}}{m_1 + m_2} g = \frac{2}{5} g $

Рассмотрим граничный случай, когда коэффициент трения минимален.
На клин действует сила $P, \vec{P} = - \vec{N_1}$ где $N_1 = m_1 g \cos{\alpha}$ сила реакции опоры которое действует на тело $m_1$
В горизонтальной проекции, на клин действует сила трения и проекция силы $\vec{P}$
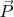
В вертикальной проекции, другая проекция силы $\vec{P} $ и тяжесть самого клина уравновешены силой реакции опоры $N$

$P \sin{\alpha} = \mu N$
$P \cos{\alpha} + M g = N$ откуда минимальныы коэффициент трения $\mu = \frac{P \sin{\alpha}}{P \cos{\alpha} + M g} = \frac{m_1 \sin{\alpha} \cos{\alpha}}{m_1 \cos{\alpha}^2 + M} = \frac{12}{59}$ против $\frac{6}{113}$ в ответе.

[mihiv]

Не учли силу, с которой на клин действует натянутая нить.