Ну тут много будет. Во-первых аксиомы булевой алгебры не совпадают с аксиомами классического исчисления высказываний и там разные названия. Но с другой стороны во-вторых у булевой алгебры вполне алгебраические названия, так что всё как по-русски, а вот с логическими аксиомами можно поразбираться.
В некоторых аксиоматиках аксиомы хорошо делятся на правила введения и удаления связок, вот например возьмём такую:
https://en.wikipedia.org/wiki/Intuitionistic_logic#Hilbert-style_calculus. Там:
• правило Modus ponens (MP) — это удаление

; введение

не входит в виде правила, но ему соответствует метатеорема о дедукции;
• AND-1, AND-2 — удаление

, AND-3 — введение

;
• OR-1, OR-2 — введение

, OR-3 — удаление

;
• FALSE — удаление

, а правила введения

не дают по смыслу этой константы;
• аналогично если бы была аксиома TRUE:

— она была бы введением

, а удаления не предусматривается;
• правило ∀-GEN — введение

, аксиома PRED-1 — удаление;
• правило ∃-GEN — удаление

, аксиома PRED-2 — введение;
• NOT-1′ можно вполне считать введением

, NOT-2′ удалением, хотя они просто являют переписывание
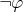
как

;
• NOT-1 — снова введение

, NOT-2 — удаление, «менее читерские»;
• IFF-1, IFF-2 — снова «читерское» удаление

, и IFF-3 — введение.
Дальше там предлагают добавить какую-нибудь аксиомку, чтобы логика стала классической, с их названиями, которые я сюда переписывать не стану. Если теперь вернуться к THEN-1 и THEN-2, они не являются ни введением, ни удалением

, но их можно называть аксиомами K и S соответственно, ибо они есть в точности типы комбинаторов K и S.
В
натуральном выводе введение и удаление импликации выходят намного естественнее (метатеорема о дедукции уже не метатеорема, а правило наряду с остальными, и эквиваленты аксиом K, S, являющиеся в некотором смысле её присутствием в системе, уже не нужны).
Если интересны названия аксиом всё же булевых алгебр, отошлю к
https://en.wikipedia.org/wiki/Boolean_algebra_(structure).
-- Пн апр 06, 2020 13:03:55 --Вообще же булевы алгебры лучше определять не длинными списками аксиом, а короткой фразой типа «[ограниченная] дистрибутивная решётка с дополнением» (ограниченность требуется дополнением, так что можно её не проговаривать), где в свою очередь решётка — это частичный порядок, у которого есть sup и inf любой пары элементов (которые и станут операциями

). Дистрибутивность и дополнение можно обдумать в терминах порядка и получить картину не хуже чем идя от одних аксиом. И лучше (всем, ставящим «булеву» алгебру во главу угла, и я кошусь немного и в сторону ТС) знать, что это не какая-то уникальная штуковина, а уникальная штуковина со связями, в частности рядом с ней ещё будет стоять например алгебра Гейтинга (Heyting), ну и что это не только одна конкретная двухэлементная структура

(ой не все в курсе этого!).
По поводу логических систем:
вот тут есть разные аксиоматизации вместе с авторством. Они больше к тому, что вы можете кого-нибудь попугать например «аксиомой Мередита» (хотя что конкретно это будет означать, зависит от того, какая из его аксиоматизаций и какой логики используется), и там ещё куча других аксиоматизаций с единственной аксиомой.
-- Пн апр 06, 2020 13:28:53 --А, чего забыл дописать: «дистрибутивная решётка с дополнением» лучше в том же ключе, как и лучше определять модуль как абелеву группу

вместе с морфизмом колец

. Да, немного придётся распаковать, зато с этими понятиями идёт сразу их применимость, а с плоским списком аксиом ничего само собой не идёт — надо будет вывести всё самому (ну или почитать такой вывод) и нигде особо не посмотришь, в отличие от лёгкости поиска по терминам. Выводить конечно тоже полезно и частью придётся везде, но.