Здравствуйте. Обнаружил интересную вещь при попытке решения следующей задачи.
Пусть

есть радиус-вектор точки в плоскости. Какая кривая выражается уравнением
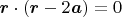
? Какое свойство этой кривой вытекает непосредственно из только что написанного уравнения кривой?
Ответ: Окружность; вписанный в окружность угол, опирающийся на диаметр, есть прямой.
С помощью построения я убедился, что мы действительно можем получить окружность
(Рис. 1)
Все точки лежат в плоскости

. Здесь роль радиус-вектора

играет вектор

, также

и угол между штриховыми прямыми прямой. Если радиус-вектор

вращать вокруг оси

, то его конец опишет окружность (нарисовано). Также показано возможность существования другой окружности (не нарисовано). Значит, когда в начале условия задачи говорится, что

есть радиус-вектор точки в плоскости, то это нужно для того, чтобы мы не получили сразу бесконечное множество окружностей, а ограничились только одной, лежащей в данной плоскости, в той, о которой говорится в начале условия задачи. Тогда ответом на первый вопрос задачи будет: окружность, лежащая в данной плоскости. Если же первое предложение из условия задачи выбросить, то ответом будет: множество разных окружностей. Подскажите, пожалуйста, правильно ли я понял наличие первого предложения в условии задачи?
Потом я решил нарисовать больше точек, аналогичных

и

и получил
(Рис. 2)
Эти точки показаны точками. (Здесь они нарисованы в плоскости

а не

.) Прослеживается, что они лежат на окружности. Сначала мне это показалось неожиданным, но позже я понял, что этот случай тоже удовлетворяет условию задачи. Рисунки я рисовал (и в итоге ограничился только одним "вариантом" вектора

), потому что не знаю пока, как решить эту задачу "в общем виде". Из исходного уравнения я могу сделать вывод, что или два вектора-сомножителя перпендикулярны между собой, либо один из них равен нулю, либо - оба. Есть расплывчатая идея взять ещё какую-то конструкцию векторов и использовать их вместе с данным уравнением, но конкретного пока ничего в голову не приходит. Буду рад, если вы подтолкнете меня в нужном направлении, чтобы я в результате смог сам прийти к ответу. Второй вопрос задачи пока можно отложить. Там у меня ещё меньше идей :)