[upd: текст этого сообщения был полностью переделан ниже с учётом замечаний, теперь уже нет смысла его смотреть здесь]
Просьба подсказать, всё ли корректно и понятно в следующем тексте. Достаточно ли подробно аргументирован ответ на вопрос в конце текста?
Пусть

-- совокупность случайных точек из
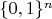
(то есть случайных последовательностей из 0 и 1 длины

). Всё равновероятно, как при бросании монетки в схеме Бернулли.
Для любого

рассмотрим все возможные пары непересекающихся подмножеств

и
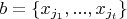
. Множество всех таких [неупорядоченных] пар обозначим

, а его мощность

(подсчёт

-- простая комбинаторная задача, но сейчас это не существенно). Для любых

вычислим их "цифровые корни" -- сумму всех координат по модулю 2. То есть цифровой корень

равен

(сумма по модулю 2).
Рассмотрим случайную величину

, равную количеству пар

, у которых цифровые корни

и

совпадают.
Вопрос: чему равно мат.ожидание

?
Ответ: мат.ожидание

равно

, поскольку все "биты" выбраны равновероятно и поэтому все 4 исхода для цифровых корней

и

также равновероятны.



