Раскрытие неопределенности вида

:
Пусть
1) Функции

и

определены и дифференцируемы в некоторой проколотой окрестности точки

;
2)

в этой окрестности точки

;
3)

;
4) Существует конечный или бесконечный предел отношения производных

.
Тогда существует предел отношения функций
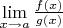
, причем

.
Раскрытие неопределенности вида

:
Пусть
1) Функции

и

определены и дифференцируемы в некоторой проколотой окрестности точки

;
2)
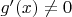
в этой окрестности точки

;
3)

;
4) Существует конечный или бесконечный предел отношения производных

.
Тогда существует предел отношения функций
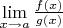
, причем

.
Можно ли доказать данную теорему на основании первой теоремы следующем образом:
Функции
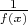
и
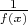
являются бесконечно малыми при

и удовлетворяют условиям первой теоремы. Тогда

Следовательно
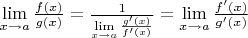
.



