Дорогие форумчане!
Помогите разобраться как доказывать единственность решений дифференциальных уравнений в частных производных. Меня в особенности интересует ситуация, когда начальная функция имеет скачок в некоторой точке.
Поскольку сообщение получилось длинным, обозначу вкратце проблему. Если функции

в уравнении (5) (ниже, в рамочке) ограничены, то можем оценить их константой, и дальше воспользоваться леммой Гронуолла-Белмана. Однако если начальная функция имеет скачок, то функции

не будут иметь ограниченные производные, и так действовать нельзя. Вопрос в том, что делать для такого случая, когда начальная функция имеет разрыв.
Ниже приведу схему как доказывать единственность в случае когда начальная функция непрерывна.
К примеру, возьмем уравнение Хопфа

и пусть

и

два решения этого уравнения, которые совпадают в начальный момент времени,

и оба существуют на каком-то интервале времени по

то есть для
![$t\in[0,T],$ $t\in[0,T],$](https://dxdy-04.korotkov.co.uk/f/f/5/3/f53f6d64930253e7f779e618a5fdca6b82.png)
где

это некоторое число.
(Решение будет существовать только для достаточно малых значений времени

; так вот, вопрос об укручении профиля и о том что решение в определенный момент перестает существовать меня не интересует, интересует только как доказывать единственность).
1. Вычтем

из
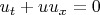
, и обозначим

тогда получим

Здесь выражение
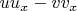
можно преобразовать двумя способами: как
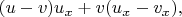
или как

Первый способ дает нам

а второй

Беря полусумму от этих двух уравнений, получаем уравнение симметричное относительно

и

 2.
2.Все три уравнения (1), (2), (3) одинаково пригодны для использования; возьмем для определенности уравнение (1).
Здесь домножаем на

и пытаемся преобразовать к виду, который будет затем удобно проинтегрировать по x по всей оси.
Получаем сперва

и, выделяя полные производные и умножая на 2, приходим к

Интегрируем по всей оси, перенося производную по

в одну сторону, и все остальные слагаемые в другую сторону,

Здесь мы предположили что

Это выполняется, к примеру, если

при

при всех
![$t\in[0,T].$ $t\in[0,T].$](https://dxdy-04.korotkov.co.uk/f/3/f/5/3f5a2a1a3bb558b887f5b62e3e74302b82.png)
Предположим что производные от решений
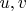
равномерно ограничены по всей оси по x, и на каком-то интервале по t; обозначим
![$M_u = \sup\limits_{x\in\mathbb{R},t\in[0,T]}|u_x(x,t)|,\qquad M_v = \sup\limits_{x\in\mathbb{R},t\in[0,T]}|v_x(x,t)|,
\qquad \mbox{ и }\quad M=\frac13\max(M_u,M_v).$ $M_u = \sup\limits_{x\in\mathbb{R},t\in[0,T]}|u_x(x,t)|,\qquad M_v = \sup\limits_{x\in\mathbb{R},t\in[0,T]}|v_x(x,t)|,
\qquad \mbox{ и }\quad M=\frac13\max(M_u,M_v).$](https://dxdy-03.korotkov.co.uk/f/a/6/7/a673aae9100ba50c60b42f363d7f055182.png)
Тогда уравнение (5) позволяет написать оценку

Обозначим

тогда неравенство интегралов переписывается как

Предположим что в какой-то точке

тогда последнее неравенство можно переписать в виде

и если

на каком-то отрезке
![$t\in[t_1,t_2],$ $t\in[t_1,t_2],$](https://dxdy-02.korotkov.co.uk/f/1/f/7/1f7ef220eece395637ef355a013fff0782.png)
включая концы, то можем проинтегрировать по отрезку
![$[t_1, t],$ $[t_1, t],$](https://dxdy-03.korotkov.co.uk/f/e/2/2/e2211f155320d04d9b33854524008d8282.png)
где

Получаем

и

и здесь нам важна лишь оценка сверху, то есть

Эта оценка получена для точки
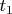
в которой

однако теперь мы можем уменьшать точку

пока не дойдем до первой точки

в которой

(Поскольку

- вследствие начального условия

, то поэтому

)
3.Итак, что же мы доказали?
Мы доказали следующую теорему.
Теорема.
Пусть  - это дифференцируемая функция, такая что существует
- это дифференцируемая функция, такая что существует 
Пусть  при
при 
Пусть, далее, ![$u(x,t), v(x,t), x\in\mathbb{R}, t\in[0,T]$ $u(x,t), v(x,t), x\in\mathbb{R}, t\in[0,T]$](https://dxdy-01.korotkov.co.uk/f/4/2/1/421a1c134140287a17bab94fd1088f4382.png) - это две непрерывные функции, имеющие в каждой точке
- это две непрерывные функции, имеющие в каждой точке  частные производные по
частные производные по  и по
и по  (в точке
(в точке 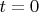 производные односторонние).
производные односторонние).
Пусть  при
при  для каждого
для каждого ![$t\in[0,T],$ $t\in[0,T],$](https://dxdy-04.korotkov.co.uk/f/f/5/3/f53f6d64930253e7f779e618a5fdca6b82.png)
и ![$\sup\limits_{x\in\mathbb{R},t\in[0,T]}|u_x(x,t)|<\infty,\qquad \sup\limits_{x\in\mathbb{R},t\in[0,T]}|v_x(x,t)|<\infty.$ $\sup\limits_{x\in\mathbb{R},t\in[0,T]}|u_x(x,t)|<\infty,\qquad \sup\limits_{x\in\mathbb{R},t\in[0,T]}|v_x(x,t)|<\infty.$](https://dxdy-02.korotkov.co.uk/f/1/3/6/1360373004849d45bb4c693e4d54889382.png)
Тогда ![$u(x,t)\equiv v(x,t),\quad x\in\mathbb{R}, t\in[0,T].$ $u(x,t)\equiv v(x,t),\quad x\in\mathbb{R}, t\in[0,T].$](https://dxdy-01.korotkov.co.uk/f/8/5/3/85389ee5aac770d88b1d89dab581fde382.png)
4.Теперь возьмем случай когда начальная функция имеет скачок в некоторой точке

Мы предполагаем что решения

,

имеют разрыв только в начальный момент времени
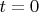
, а затем они становятся гладкими.
Мы тогда опять приходим к уравнению (5) (выше, в рамочке), но теперь мы не можем предполагать что
![$\sup\limits_{t\in[0,T]}|u_x|$ $\sup\limits_{t\in[0,T]}|u_x|$](https://dxdy-02.korotkov.co.uk/f/1/7/7/1774db5d697c8a23fbe841856104278682.png)
ограничен, так как в точках

близких к

производная

будет расти при

Вопрос что делать в этом случае.
Буду благодарен за ответы.



